Triangolo di Tartaglia
Con il binomio di Newton abbiamo visto che è possibile calcolare la potenza n-esima di un qualsiasi binomio. Abbiamo però notato che può risultare abbastanza faticoso calcolare i vari coefficienti binomiali, infatti se ad esempio vogliamo calcolare una potenza settima dobbiamo trovare ben \(8\) coefficienti binomiali.
Esiste un modo per calcolare tali coefficienti direttamente?
E' possibile trovare direttamente tali coefficienti utilizzando il triangolo di Tartaglia. Rappresenta un vero e proprio triangolo dove ad ogni riga abbiamo dei coefficienti
Ovviamente il triangolo ha potenzialmente righe infinite, possiamo sempre ricavare quella successiva.
Ogni riga rappresenta i coefficienti di una potenza di binomio, si parte dalla riga 1 che rappresenta la potenza \((a+b)^0\). Man mano che scendiamo di righe la potenza aumenta di \(1\), quindi ad esempio la riga \(3\) rappresenta la potenza \((a+b)^2\).
Noi sappiamo che \((a+b)^2=a^2+2ab+b^2\) e possiamo notare il fatto che i coefficienti dei singoli monomi sono \(1\) \(2\) e \(1\), proprio i valori che troviamo nella riga \(3\) del triangolo.
Trucco mnemonico
Bisogna ricordare il triangolo a memoria? Ovviamente no, esiste un modo per ricavarlo a partire dalla riga \(1\), come mostrato in figura
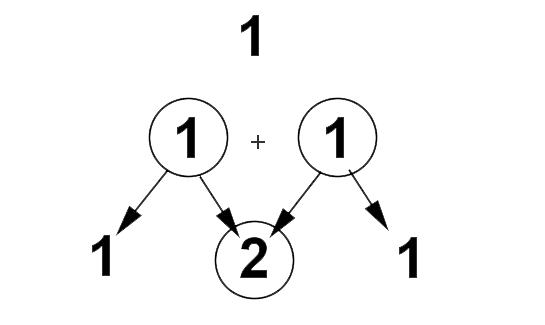Si procede nel seguente modo:
Si parte dalla prima riga scrivendo il valore \(1\), la riga successiva avrà \(1\) e \(1\), alla terza riga avremo \(1\), \(1+1\) e \(1\). In sostanza in ogni riga il primo e ultimo valore sono sempre \(1\), quelli intermedi sono dati da varie somme, infatti alla quarta riga avremo \(1\), \((1+2)\), \((2+1)\), \(1\), e cosi via.
Esempio svolto
$$ (a+b)^6 $$ E' sufficiente prendere la riga \(6+1=7\) per trovare i coefficienti. I coefficienti quindi sono \(1\hspace{3mm} 6\hspace{3mm} 15\hspace{3mm} 20\hspace{3mm} 15\hspace{3mm} 6\hspace{3mm} 1\). Usando anche le nozioni viste con il binomio di Newton possiamo dunque scrivere che $$ (a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6 $$ $$ (a+b)^6 $$ $$ \Downarrow $$ $$ a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6 $$ $$ (a+b)^6 $$ $$ \Downarrow $$ $$ a^6+6a^5b+15a^4b^2+ $$ $$ +20a^3b^3+15a^2b^4+6ab^5+b^6 $$
Esiste un modo per calcolare tali coefficienti direttamente?
E' possibile trovare direttamente tali coefficienti utilizzando il triangolo di Tartaglia. Rappresenta un vero e proprio triangolo dove ad ogni riga abbiamo dei coefficienti
Noi sappiamo che \((a+b)^2=a^2+2ab+b^2\) e possiamo notare il fatto che i coefficienti dei singoli monomi sono \(1\) \(2\) e \(1\), proprio i valori che troviamo nella riga \(3\) del triangolo.
Trucco mnemonico Bisogna ricordare il triangolo a memoria? Ovviamente no, esiste un modo per ricavarlo a partire dalla riga \(1\), come mostrato in figura
Si parte dalla prima riga scrivendo il valore \(1\), la riga successiva avrà \(1\) e \(1\), alla terza riga avremo \(1\), \(1+1\) e \(1\). In sostanza in ogni riga il primo e ultimo valore sono sempre \(1\), quelli intermedi sono dati da varie somme, infatti alla quarta riga avremo \(1\), \((1+2)\), \((2+1)\), \(1\), e cosi via.
Esempio svolto $$ (a+b)^6 $$ E' sufficiente prendere la riga \(6+1=7\) per trovare i coefficienti. I coefficienti quindi sono \(1\hspace{3mm} 6\hspace{3mm} 15\hspace{3mm} 20\hspace{3mm} 15\hspace{3mm} 6\hspace{3mm} 1\). Usando anche le nozioni viste con il binomio di Newton possiamo dunque scrivere che $$ (a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6 $$ $$ (a+b)^6 $$ $$ \Downarrow $$ $$ a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6 $$ $$ (a+b)^6 $$ $$ \Downarrow $$ $$ a^6+6a^5b+15a^4b^2+ $$ $$ +20a^3b^3+15a^2b^4+6ab^5+b^6 $$
Esercizi di Matematica
Film Matematici
Formulari di Matematica
Calcolatori Matematici
Ebook
Paradossi
Podcast
