L'insieme dei numeri naturali è l'insieme formato dagli elementi $$ \mathbb{N}=\{0,1,2,3,4,5......\infty\} $$ Su questo insieme vengono definite l'operazione classica di somma e di prodotto.
L'operazione di somma gode delle seguenti proprietà:

• \(a+b=b+a\rightarrow\) Proprietà commutativa
• \((a+b)+c=a+(b+c)\rightarrow\) Proprietà associativa
• \(0+a=a\rightarrow\) Elemento neutro
• \(a+b=c+b\Rightarrow a=c\rightarrow\) Legge di cancellazione (b si può eliminare)

L'operazione di prodotto gode delle seguenti proprietà:

• \(a\cdot b=b\cdot a\rightarrow\) Proprietà commutativa
• \((a\cdot b)\cdot c=a\cdot(b\cdot c)\rightarrow\) Proprietà associativa
• \(1\cdot a=a\rightarrow\) Elemento neutro
• \(a\cdot(b+c)=a\cdot b+a\cdot c\rightarrow\) Proprietà distributiva rispetto alla somma
• \(a\cdot b=0\Rightarrow a=0\hspace{2mm}oppure\hspace{2mm} b=0 \rightarrow\) Legge di annullamento del prodotto

Consideriamo due numeri naturali \(a\) e \(b\). E' sempre possibile definire un ordine, cioè identificare il più piccolo e il più grande. Matematicamente $$ se\hspace{2mm}a\geq b\Rightarrow \exists n\in \mathbb{N}| b+n=a $$ Se prendiamo i numeri 42 e 22, sappiamo che $$ 42\geq 22 $$ Dunque $$ n=20 $$ Se \(a\) divide \(b\) significa che esiste un numero naturale che moltiplicato per \(a\) restituisce \(b\). Matematicamente $$ se\hspace{2mm}a\hspace{2mm}divide\hspace{2mm} b\Rightarrow \exists n\in \mathbb{N}| a\cdot n=b $$ $$ se\hspace{2mm}a\hspace{2mm}divide\hspace{2mm} b\Rightarrow \exists n\in \mathbb{N}| a\cdot n=b $$ $$ se\hspace{2mm}a\hspace{2mm}divide\hspace{2mm} b\Rightarrow \exists n\in \mathbb{N}| a\cdot n=b $$ In questo caso \(a\) è un divisore di \(b\) e \(b\) è un multiplo di \(a\).
Se un numero ha come divisori soltanto 1 e se stesso allora si parla di numero primo. I numeri primi hanno una importanza assoluta in matematica, in quanto sono i mattoni, rappresentano la base per costruire tutti i numeri. In particolare un qualsiasi numero naturale maggiore di 1 può essere scritto come prodotto di numeri primi e tale prodotto è unico! (teorema fondamentale dell'aritmetica)
Un qualsiasi numero può essere scomposto in fattori primi, cioè scomposto in modo da scrivere il numero come prodotto di un certo numero di fattori rappresentati per l'appunto da numeri primi. Qui di seguito vengono mostrate tre scomposizioni
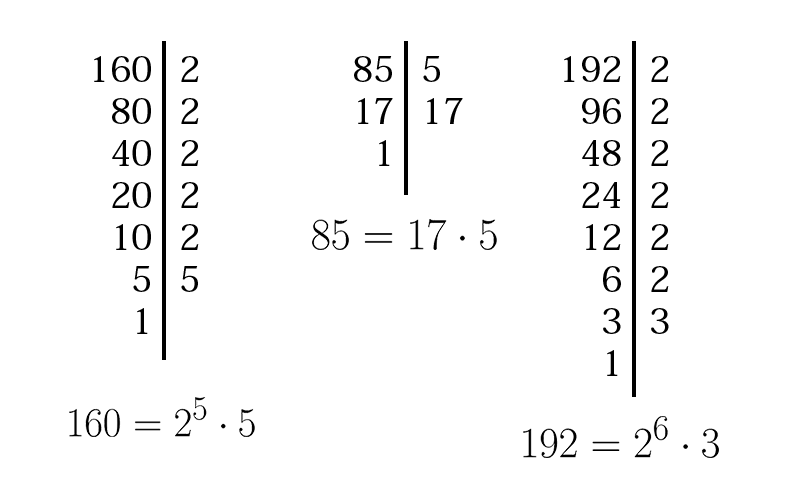
Ricordiamo infine che sui numeri naturali si possono calcolare il massimo comun divisore (MCD) e il minimo comune multiplo (mcm).
Per calcolare il MCD bisogna scomporre tutti i numeri in fattori primi e prendere tutti i fattori comuni, presi una sola volta, con il più piccolo degli esponenti. Non dimentichiamoci il fatto che MCD indica il numero massimo che è in grado di dividere tutti i numeri in questione.
Per calcolare il mcm bisogna scomporre tutti i numeri in fattori primi e prendere tutti i fattori comuni e non comuni, presi una sola volta, con il più grande degli esponenti. Non dimentichiamoci il fatto che mcm indica il numero minimo che è in grado di essere diviso da tutti i numeri in questione, il multiplo più piccolo.

---

Dalla quotidianità sappiamo che molto spesso è necessario svolgere una operazione di sottrazione. Ad esempio se ho 5 mele e ne regalo 3 me ne restano 2, perchè semplicemente ho fatto \(5-3=2\). Il problema è che questa operazione di sottrazione non può essere fatta sempre se ci troviamo nel campo dei numeri naturali. Supponiamo di voler risolvere la seguente equazione nel campo dei neturali $$ x+3=0 $$ Bisogna trovare un numero naturale che sostituito alla x e sommato a 3 dia come risultato il numero 0. Sappiamo tutti che questa cosa è impossibile!!La soluzione di questa equazione è \(x=-3\) che non rientra nei numeri naturali.
Vi è capitato sicuramente di andare in negativo sul vostro conto bancario o sulla vostra sim del cellulare. Ebbene quel valore non può essere rappresentato dai numeri naturali, semplicemente perchè non esiste il concetto di numero negativo.
Nasce la necessità di introdurre un nuovo insieme indicato con \(\mathbb{Z}\) chiamato interi relativi e sono tutti i numeri visti nei naturali preceduti però dai segni meno $$ \mathbb{Z}=\{0,\pm1,\pm2,\pm3,\pm4,\pm5......\pm\infty\} $$ $$ \mathbb{Z}=\{0,\pm1,\pm2,\pm3,\pm4,\pm5......\pm\infty\} $$ $$ \mathbb{Z}=\{0,\pm1,\pm2,\pm3,\pm4,\pm5....\pm\infty\} $$ Anche in questo insieme vengono definite l'operazione di somma e di prodotto e anche in questo caso valgono le stesse proprietà viste nei naturali. Viene però aggiunta una proprietà fondamentale, cioè esiste per numero intero relativo il suo opposto, matematicamente $$ \forall z\in\mathbb{Z} \exists z'\in\mathbb{Z}| z+z'=0 $$ L'opposto di un numero coincide con il numero di partenza cambiato di segno, se era positivo diventa negativo e viceversa.
Dati due numeri interi relativi, anche qui è possibile fornire un ordinamento, cioè è possibile stabilire il valore più grande e il più piccolo. Semplicemente ogni numero positivo è più grande di tutti i numeri negativi, inoltre tra numeri negativi è più grande quello che è meno negativo, cioè quello con il valore numerico (senza contare il segno) più piccolo
Come si svolge concretamente l'operazione di somma? Nulla di più semplice in realtà. Se i numeri hanno lo stesso segno allora si ricopia il segno e si effettua la somma classica tra i valori. Se sono di segno discorde vince il segno del numero con valore più alto e si effettua la differenza classica.
Per il prodotto bisogna moltiplicare semplicemente i valori, tenendo presente che bisogna anche fare il prodotto dei segni, riassunto nel seguente modo
Supponiamo di voler dividere una caramella in due parti uguali, in modo da accontentare due bambini. Nulla di più semplice!
In realtà il risultato di questa operazione non è esprimibile utilizzando i numeri interi relativi, in quanto entrano in scena altri oggetti matematici. Proviamo a risolvere la seguente equazione $$ 2x=1 $$ Bisogna trovare un numero intero relativo che sostituito alla x e moltiplicato per 2 ci fornisce come risultato 1. Sappiamo benissimo che questa è impossibile!
Il risultato di questa equazione è infatti \(x=\frac{1}{2}\) che non rientra nei numeri interi relativi.