Consideriamo una certa funzione \(f(x)\). Vogliamo trovare una nuova funzione \(F(x)\) fatta in modo che la sua derivata coincida con la funzione di partenza. In altri termini $$ F'(x)=f(x) $$ La funzione \(F(x)\) si chiama primitiva di \(f(x)\). Una volta trovata una primitiva, in realtà ne abbiamo trovate infinite.
Ci ricordiamo infatti che la derivata di una costante è pari a 0 e questo implica che se sommiamo una costante alla primitiva, non cambia il suo ruolo infatti $$ F'(x)=\frac{d}{dx}(F(x)+c) $$ Si definisce integrale indefinito di \(f(x)\) l'insieme di tutte le sue primitive, in formule $$ \int f(x)dx=F(x)+c $$ Il simbolo di integrale è \(\int\). La funzione \(f(x)\) si chiama integranda.
La domanda è: come si trova la primitiva di una funzione?
Esistono in realtà delle tecniche per trovare la primitiva (oggetto di un corso di analisi matematica). In genere gli integrali che si incontrano in fisica, sono immediati.

---

Consideriamo la seguente funzione \(f(x)\)
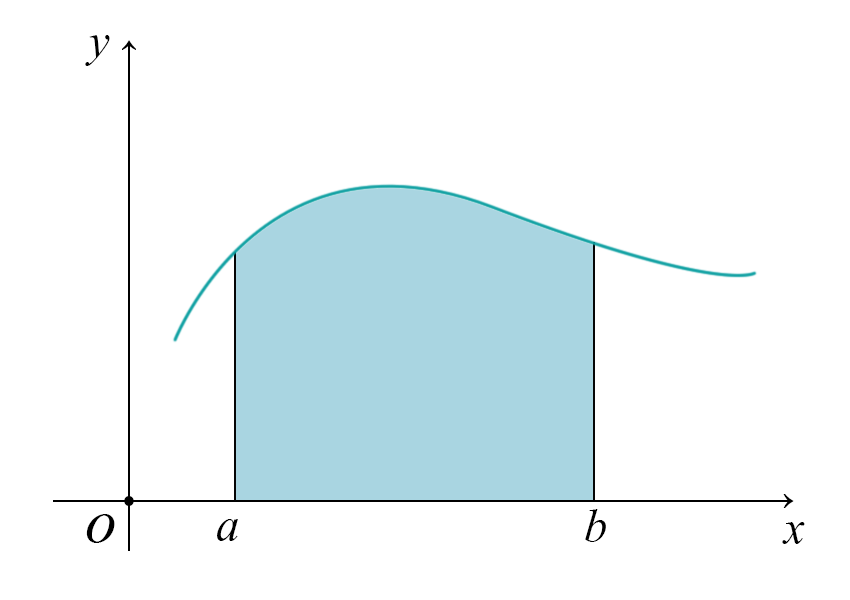
Vogliamo capire quant'è l'area della regione di spazio delimitata dalla funzione, da \(a\) e da \(b\). Come si procede?
Prendiamo \(a\) e \(b\) e dividiamo questa regione di spazio in segmenti. Vengono fuori dei rettangoli, come mostrato in figura
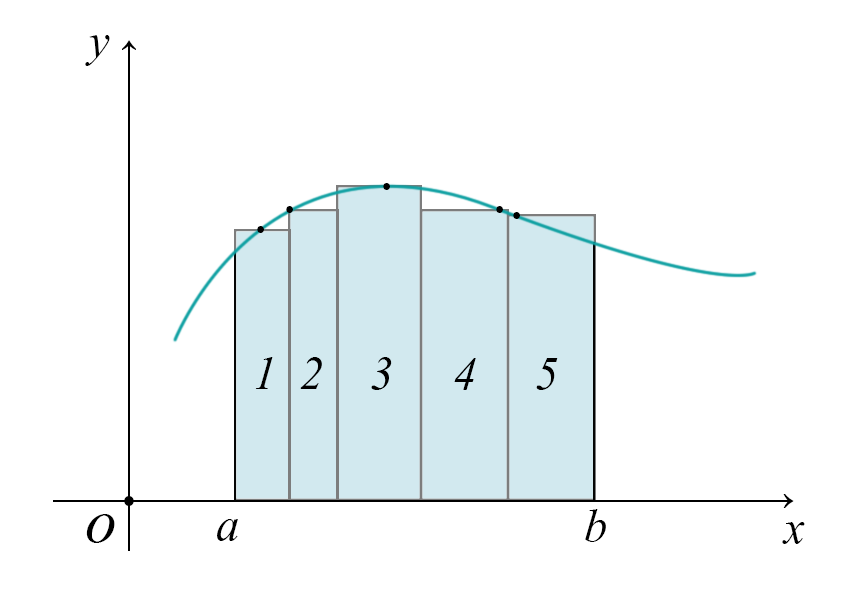
Una stima dell'area che stiamo cercando, coincide con la somma delle aree dei rettangoli disegnati, in formule $$ A_{stimata}=\sum_{1}^{5}A_{i} $$ Dove \(A_i\) rappresenta l'area del rettangolo i-esimo $$ A_{i}=f_i\cdot \Delta x_i $$ La \(f_i\) è il valore della funzione nel punto i-esimo, mentre \(\Delta x_i\) è l'ampiezza dell'intervallo, cioè la base del rettangolo.
Si vede dal grafico che a volte sovrastimiamo la scelta del rettangolo, il quale avrà un'area in surplus, mentre a volte ci sarà una parte di area non coperta dal rettangolo.
Inoltre la scelta del numero di rettangoli e dell'altezza del rettangolo stesso, è arbitraria. Per ovviare a questi problemi, si può pensare di aumentare il numero di rettangoli e di ridurne la larghezza.
In particolare quando il numero di rettangoli tende ad infinito e la larghezza tende a zero, otteniamo un integrale definito, in formule $$ A_{stimata}=\sum_{i=1}^{N}f_i\Delta x_i\xrightarrow[N\rightarrow \infty]{\Delta x\rightarrow 0} \int_{a}^{b}f(x)dx $$ $$ A_{stimata}=\sum_{i=1}^{N}f_i\Delta x_i\xrightarrow[N\rightarrow \infty]{\Delta x\rightarrow 0} \int_{a}^{b}f(x)dx $$ $$ A_{stimata} $$ $$ \Downarrow $$ $$ \sum_{i=1}^{N}f_i\Delta x_i\xrightarrow[N\rightarrow \infty]{\Delta x\rightarrow 0} \int_{a}^{b}f(x)dx $$ L'integrale definito ha la stessa scrittura di quello indefinito, con la differenza che qui abbiamo quelli che si chiamano estremi di integrazione. L'estremo inferiore è \(a\), quello superiore è \(b\).
L'integrale definito dunque è la somma di rettangoli di base \(dx\) e altezza \(f(x)\). Questo spiega l'utilizzo di \(\int\) per indicare l'integrale, in quanto è riferito al simbolo di somma stilizzato.
Ovviamente esiste una relazione tra l'integrale definito e l'integrale indefinito data dal teorema fondamentale del calcolo integrale:
L’integrale definito di una funzione continua, calcolato nell’intervallo \((a,b)\), è uguale alla differenza tra i valori che una qualunque primitiva di \(f(x)\) assume agli estremi superiore e inferiore dell’intervallo d’integrazione, in formule $$ \int_{a}^{b}f(x)dx=F(b)-F(a) $$ Esiste un altro teorema molto importante sugli integrali, il teorema della media integrale
Questo teorema afferma che se una certa funzione è integrabile, allora nell'intervallo di integrazione esiste un punto \(c\) "speciale", cioè $$ \exists c\in [a,b] \hspace{5mm} tale \hspace{3mm} che $$ $$ f(c)=\frac{1}{b-a}\int_{a}^{b}f(x)dx $$

---

Vediamo due esercizi svolti in modo da prendere un pò di dimestichezza