In fisica esistono delle grandezze che possono dipendere da più variabili, ad esempio una funzione dipendente dalle variabili x e y $$ f(x,y) $$ Oppure possiamo incontrare una funzione che dipende da tre variabili $$ f(x,y,z) $$ Come abbiamo già visto nel capitolo sulle derivate, per una funzione \(f(x)\) abbiamo $$ \frac{df}{dx}=\lim_{\Delta x \mapsto 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} $$ $$ \frac{df}{dx}=\lim_{\Delta x \mapsto 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} $$ $$ \frac{df}{dx}=\lim_{\Delta x \mapsto 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} $$ Vogliamo adesso estendere questo concetto a funzioni in più variabili. Partiamo con la costruzione di un grafico per \(f(x,y)\), dove \((x,y)\) è il piano delle variabili indipendenti, mentre la terza dimensione è il valore della funzione Come si vede dalla figura, quella che facciamo variare inizialmente è solo la variabile \(x\), mentre la \(y\) rimane invariata. Avremo dunque la funzione \(f(x_{0},y_{0})\) e la funzione \(f(x_{0}+\Delta x,y_{0})\).
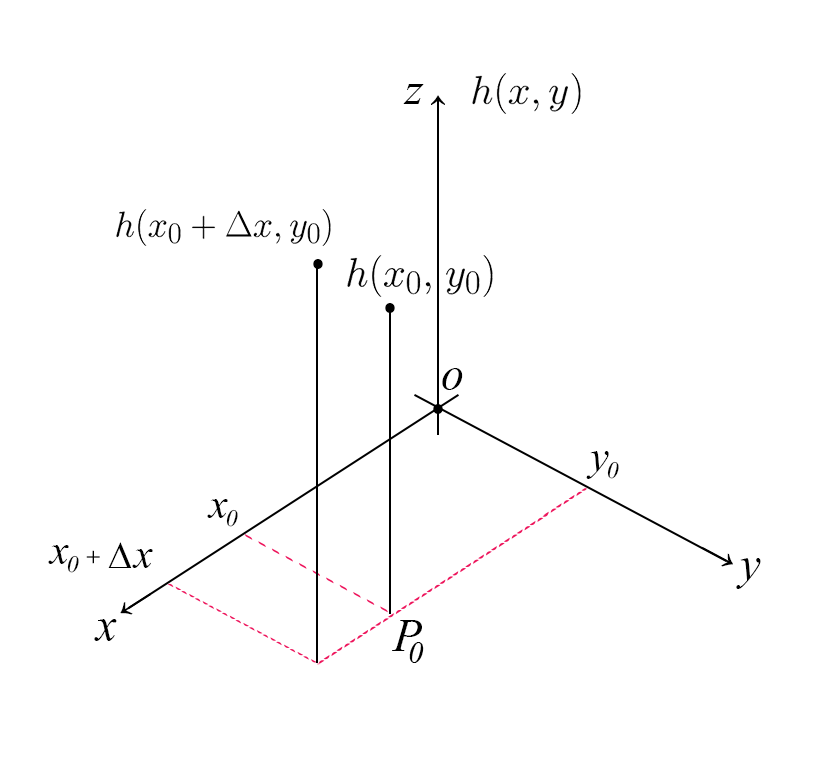
Visto che si ha una variazione, possiamo costruire il rapporto incrementale sulla variabile \(x\) $$ \frac{\Delta f}{\Delta x}=\frac{f(x_{0}+\Delta x,y_{0})-f(x_{0},y_{0})}{\Delta x} $$ $$ \frac{\Delta f}{\Delta x}=\frac{f(x_{0}+\Delta x,y_{0})-f(x_{0},y_{0})}{\Delta x} $$ $$ \frac{\Delta f}{\Delta x}=\frac{f(x_{0}+\Delta x,y_{0})-f(x_{0},y_{0})}{\Delta x} $$ Questa scrittura rappresenta la variazione di \(f(x,y)\) rispetto a \(x\). Calcoliamo adesso il limite $$ \lim_{\Delta x \mapsto 0}\frac{f(x_{0}+\Delta x,y_{0})-f(x_{0},y_{0})}{\Delta x} $$ $$ \lim_{\Delta x \mapsto 0}\frac{f(x_{0}+\Delta x,y_{0})-f(x_{0},y_{0})}{\Delta x} $$ $$ \lim_{\Delta x \mapsto 0}\frac{f(x_{0}+\Delta x,y_{0})-f(x_{0},y_{0})}{\Delta x} $$ Questo limite è la derivata parziale di \(f(x,y)\) rispetto a \(x\) nel punto \((x_{0},y_{0})\).
Il simbolo di derivata parziale è \(\partial\), dunque per indicare la derivata parziale rispetto a \(x\) si può scrivere $$ \frac{\partial f}{\partial x} $$ Facciamo la stessa operazione di prima, variando questa volta la \(y\) e mantenendo invariata la \(x\) La derivata parziale di \(f(x,y)\) rispetto a \(y\) nel punto \((x_{0},y_{0})\) è $$ \frac{\partial f}{\partial y}=\lim_{\Delta y \mapsto 0}\frac{f(x_{0},y_{0}+\Delta y)-f(x_{0},y_{0})}{\Delta y} $$ $$ \frac{\partial f}{\partial y}=\lim_{\Delta y \mapsto 0}\frac{f(x_{0},y_{0}+\Delta y)-f(x_{0},y_{0})}{\Delta y} $$ $$ \frac{\partial f}{\partial y}=\lim_{\Delta y \mapsto 0}\frac{f(x_{0},y_{0}+\Delta y)-f(x_{0},y_{0})}{\Delta y} $$ Supponiamo di avere una funzione in tre variabili \(f(x,y,z)\). Il procedimento sarà lo stesso.
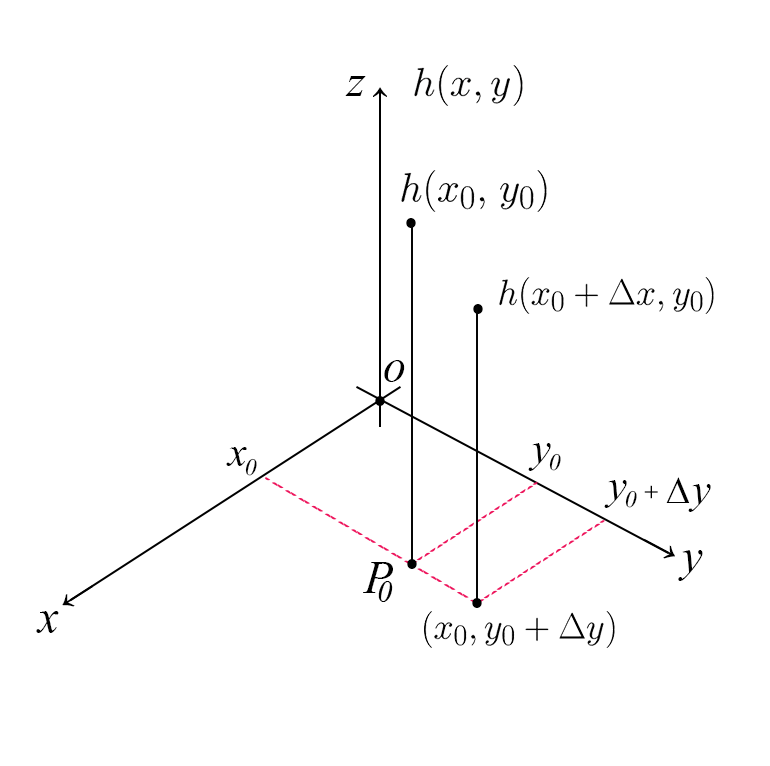
Se vogliamo calcolare la derivata parziale rispetto a \(z\) dobbiamo tenere ferme la \(x\) e la \(y\) $$ \frac{\partial f}{\partial x}=\lim_{\Delta x \mapsto 0}\frac{f(x_{0}+\Delta x,y_{0},z_{0})-f(x_{0},y_{0},z_{0})}{\Delta x} $$ $$ \frac{\partial f}{\partial y}=\lim_{\Delta y \mapsto 0}\frac{f(x_{0},y_{0}+\Delta y,z_{0})-f(x_{0},y_{0},z_{0})}{\Delta y} $$ $$ \frac{\partial f}{\partial z}=\lim_{\Delta z \mapsto 0}\frac{f(x_{0},y_{0},z_{0}+\Delta z)-f(x_{0},y_{0},z_{0})}{\Delta z} $$ $$ \frac{\partial f}{\partial x}=\lim_{\Delta x \mapsto 0}\frac{f(x_{0}+\Delta x,y_{0},z_{0})-f(x_{0},y_{0},z_{0})}{\Delta x} $$ $$ \frac{\partial f}{\partial y}=\lim_{\Delta y \mapsto 0}\frac{f(x_{0},y_{0}+\Delta y,z_{0})-f(x_{0},y_{0},z_{0})}{\Delta y} $$ $$ \frac{\partial f}{\partial z}=\lim_{\Delta z \mapsto 0}\frac{f(x_{0},y_{0},z_{0}+\Delta z)-f(x_{0},y_{0},z_{0})}{\Delta z} $$ $$ \frac{\partial f}{\partial x}=\lim_{\Delta x \mapsto 0}\frac{f(x_{0}+\Delta x,y_{0},z_{0})-f(x_{0},y_{0},z_{0})}{\Delta x} $$ $$ \frac{\partial f}{\partial y}=\lim_{\Delta y \mapsto 0}\frac{f(x_{0},y_{0}+\Delta y,z_{0})-f(x_{0},y_{0},z_{0})}{\Delta y} $$ $$ \frac{\partial f}{\partial z}=\lim_{\Delta z \mapsto 0}\frac{f(x_{0},y_{0},z_{0}+\Delta z)-f(x_{0},y_{0},z_{0})}{\Delta z} $$ Esiste la possibilità di derivare ulteriormente le derivate parziali, dando origine alle derivate parziali miste. Facciamo subito un esempio pratico per capire il tutto. Se la funzione non è patologica, vale il teorema di Schwarz, cioè le derivate seconde miste coincidono $$ \frac{\partial^2 f}{\partial y\partial x}=\frac{\partial^2 f}{\partial x\partial y} $$ $$ \frac{\partial^2 f}{\partial y\partial x}=\frac{\partial^2 f}{\partial x\partial y} $$ $$ \frac{\partial^2 f}{\partial y\partial x}=\frac{\partial^2 f}{\partial x\partial y} $$

---

Vediamo due esercizi svolti in modo da prendere un pò di dimestichezza

---

Consideriamo una funzione in due variabili \(f(x,y)\). Supponiamo di conoscere la funzione nel punto \((x_{0},y_{0})\).
Quanto vale la funzione nel punto \((x_{0}+\Delta x,y_{0}+\Delta y)\)?
Utilizziamo il teorema di Taylor $$ f(x_{0}+\Delta x,y_{0}+\Delta y) $$ $$ \Downarrow $$ $$ f(x_{0},y_{0})+\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\right]+\frac{1}{2!}\left[\frac{\partial^2 f}{\partial x^2}\Delta x^2+2\frac{\partial^2 f}{\partial x\partial y}\Delta x\Delta y+\frac{\partial^2 f}{\partial y^2}\Delta y^2\right]+... $$ $$ f(x_{0}+\Delta x,y_{0}+\Delta y) $$ $$ \Downarrow $$ $$ f(x_{0},y_{0})+\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\right]+ $$ $$ + \frac{1}{2!}\left[\frac{\partial^2 f}{\partial x^2}\Delta x^2+2\frac{\partial^2 f}{\partial x\partial y}\Delta x\Delta y+\frac{\partial^2 f}{\partial y^2}\Delta y^2\right]+... $$ $$ f(x_{0}+\Delta x,y_{0}+\Delta y) $$ $$ \Downarrow $$ $$ f(x_{0},y_{0}) + $$ $$ + \left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\right]+ $$ $$ + \frac{1}{2!}\left[\frac{\partial^2 f}{\partial x^2}\Delta x^2+2\frac{\partial^2 f}{\partial x\partial y}\Delta x\Delta y+\frac{\partial^2 f}{\partial y^2}\Delta y^2\right]+... $$ Ogni derivata parziale viene calcolata nel punto \((x_{0},y_{0})\). Il primo e il secondo pezzo della formula rappresentano la stima lineare $$ f_{stimalineare}(x_{0}+\Delta x,y_{0}+\Delta y)=f(x_{0},y_{0})+\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\right] $$ $$ f_{stimalineare}(x_{0}+\Delta x,y_{0}+\Delta y) $$ $$ \Downarrow $$ $$ f(x_{0},y_{0})+\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\right] $$ $$ f_{stima \\ lineare}(x_{0}+\Delta x,y_{0}+\Delta y) $$ $$ \Downarrow $$ $$ f(x_{0},y_{0})+\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\right] $$ In una funzione a tre variabili \(f(x,y,z)\) avremo una stima lineare fatta in questo modo $$ f_{stimalineare}(x_{0}+\Delta x,y_{0}+\Delta y,z_{0}+\Delta z)=f(x_{0},y_{0},z_{0})+\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z\right] $$ $$ f_{stimalineare}(x_{0}+\Delta x,y_{0}+\Delta y,z_{0}+\Delta z) $$ $$ \Downarrow $$ $$ f(x_{0},y_{0},z_{0})+ $$ $$ +\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z\right] $$ $$ f_{\small stima \\ lineare}(x_{0}+\Delta x,y_{0}+\Delta y,z_{0}+\Delta z) $$ $$ \Downarrow $$ $$ f(x_{0},y_{0},z_{0})+ $$ $$ +\left[\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z\right] $$