Sistemi di riferimento
Come individuare un punto P
L'idea di Cartesio era quella di poter individuare un punto in maniera non ambigua. L'obiettivo, dunque, è quello di trovare un modo per individuare un punto generico P. Scegliamo un punto di riferimento O (origine) in maniera del tutto arbitraria, siamo noi a decidere dove prendere tale punto. Questo significa che ognuno sceglie l'origine che vuole.
La domanda sorge spontanea : come troviamo la posizione del punto P rispetto all'origine O che abbiamo scelto?
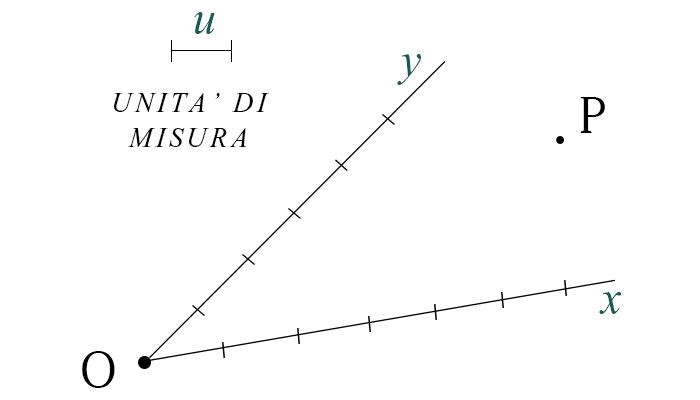
Per descrivere un punto nel piano, è necessario scegliere due direzioni. Tracciamo quindi due semirette che individuano rispettivamente le direzioni, che chiameremo direzione x e direzione y. Bisogna inoltre scegliere l'unità di misura, cioè come viene diviso l'asse x.
Se siamo su un foglio a quadretti, possiamo dire che come unità di misura prendiamo due quadratini. Si tratta comunque di una scelta arbitraria. Facciamo la stessa cosa anche sull'asse y.
Il fatto di aver diviso i due assi usando la stessa unità di misura, è anche questa una scelta, non è obbligatorio. Potete immaginare che facendo in questo modo, la trattazione si semplifica
Coordinate del punto
Assegniamo al punto una coppia di numeri. In questo modo troviamo la posizione di P rispetto a O in maniera non ambigua. Esistono due modi per trovare i due numeri, che in realtà rappresentano le coordinate x e y del punto P:
- Metodo delle parallele
Per trovare la coordinata x bisogna tracciare una retta parallela all'asse y passante per il punto P.
L'intersezione tra tale retta e l'asse x rappresenta la coordinata x del punto P.
Per trovare la coordinata y bisogna tracciare una retta parallela all'asse x passante per il punto P.
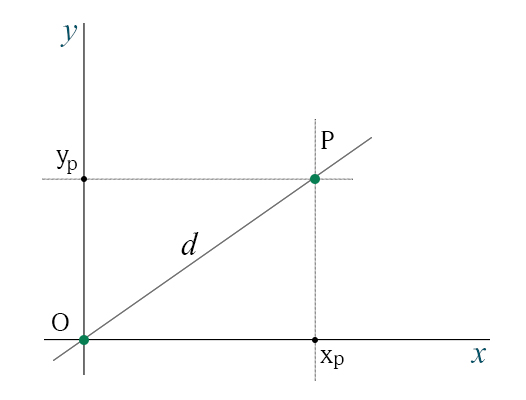
L'intersezione tra tale retta e l'asse y rappresenta la coordinata y del punto P.Dalla figura appena mostrata, si evince che il punto P si trova a x=2.5 e y=3, rispetto al punto O e alle direzioni usate.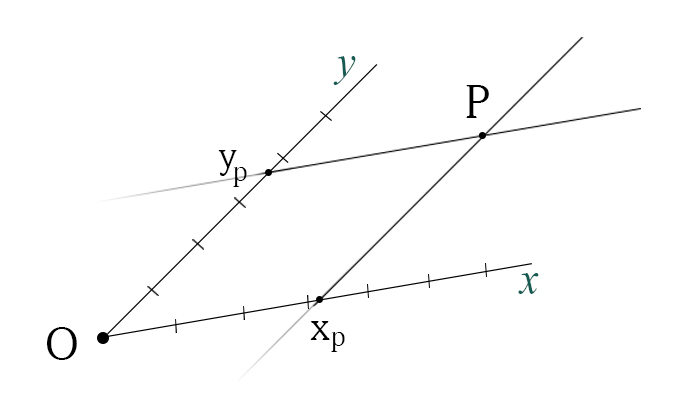
Se cambiamo direzioni, il punto P avrà coordinate diverse, anche se l'origine O rimane la stessa.
Quando dobbiamo trovare la posizione del punto P, bisogna fare diverse scelte arbitrarie:
1. Scelta del punto O di origine;
2. Scelta delle due direzioni;
3. Scelta delle unità di misura, che possono essere uguali sui due assi, oppure no. - Metodo delle perpendicolari
Per trovare la coordinata x bisogna tracciare una retta perpendicolare all'asse x passante per il punto P.
L'intersezione tra tale retta e l'asse x rappresenta la coordinata x del punto P.
Per trovare la coordinata y bisogna tracciare una retta perpendicolare all'asse y passante per il punto P.
L'intersezione tra tale retta e l'asse y rappresenta la coordinata y del punto P.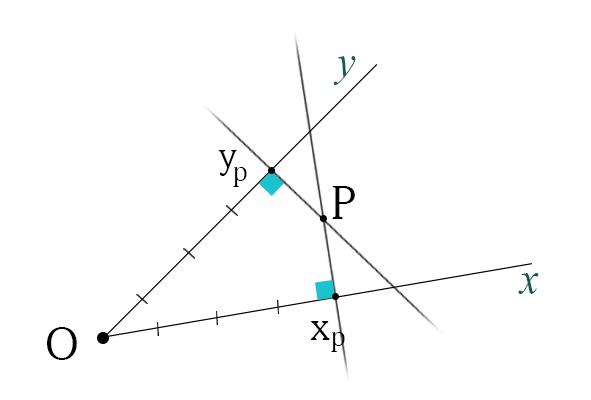
Assi cartesiani perpendicolari
Cosa succede se le direzioni degli assi sono perpendicolari tra loro? Significa dire che questa volta, non prendiamo due direzioni (x e y) casuali, ma le prendiamo in modo da avere l'asse x perpendicolare all'asse y.
Il metodo delle parallele e quello delle perpendicolari coincidono, il punto avrà le stesse coordinate, indipendentemente dal metodo usato.
Si nota infatti che la parallela all'asse y (che bisognava tracciare per trovare la coordinata x con il metodo delle parallele) coincide con la perpendicolare all'asse x (che bisognava tracciare per trovare la coordinata x con il metodo delle perpendicolari). Stessa cosa succede per la coordinata y
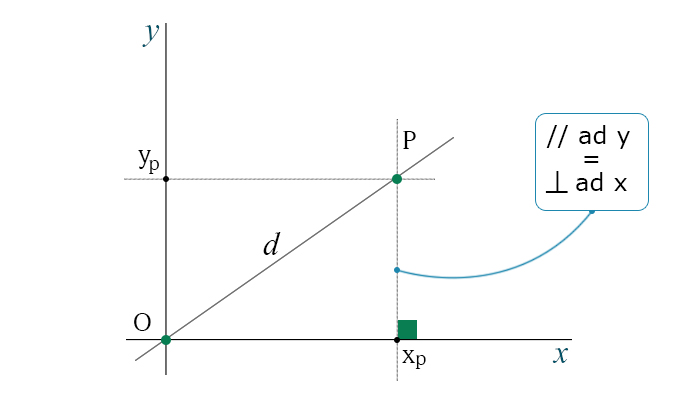
Questo è uno dei motivi per il quale tutti usiamo, senza saperlo, assi cartesiani con direzioni perpendicolari tra loro.
Ricordiamo che l'idea di Cartesio era quella di scegliere un sistema di assi cartesiani dove vengono usate direzioni qualsiasi e dove viene fissato un punto di origine O.
Dunque non è obbligatorio scegliere gli assi perpendicolari tra loro, lo si fa in automatico, ma non bisogna dimenticarsi che non è un regola fissa, ma è semplicemente un metodo comodo, che semplifica le cose.
Esiste un altro motivo che porta alla scelta di assi perpendicolari. Prendiamo un punto P e un sistema di assi non perpendicolari. Tracciamo le coordinate del punto usando il metodo delle perpendicolari, come mostrato in figura
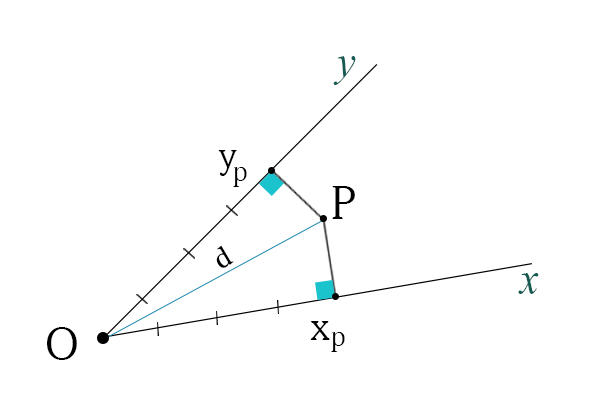
Il teorema di Pitagora lo possiamo usare se e solo se stiamo usando la stessa unità di misura, sia per x, sia per y. Se usiamo unità di misura differenti, Pitagora non si può usare in maniera immediata.
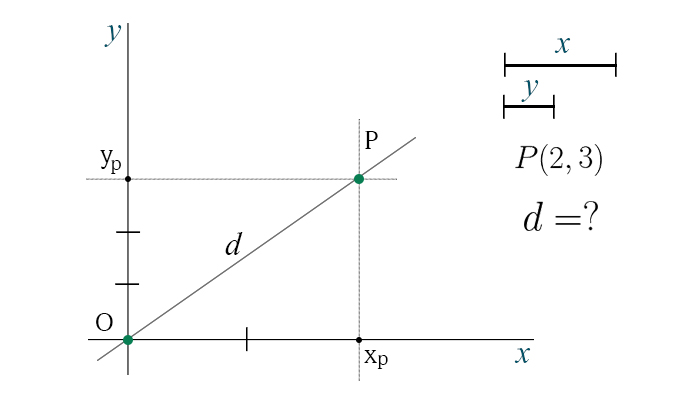
Bisogna questa volta specificare anche quale unità di misura stiamo usando. Si converte una unità di misura nell'altra, in modo da riferirci ad una unica unità. Ad esempio convertiamo l'unità di y nell'unità di x, ricordando che due unità di y coincidono con una unità di x. Se non facciamo questa conversione la formula di Pitagora non ha senso.
E' utile, ma non obbligatorio, usare assi cartesiani perpendicolari tra loro e con la stessa unità di misura.







