Prendiamo un sistema di assi cartesiani perpendicolari tra loro. Disegniamo un cerchio di raggio 1
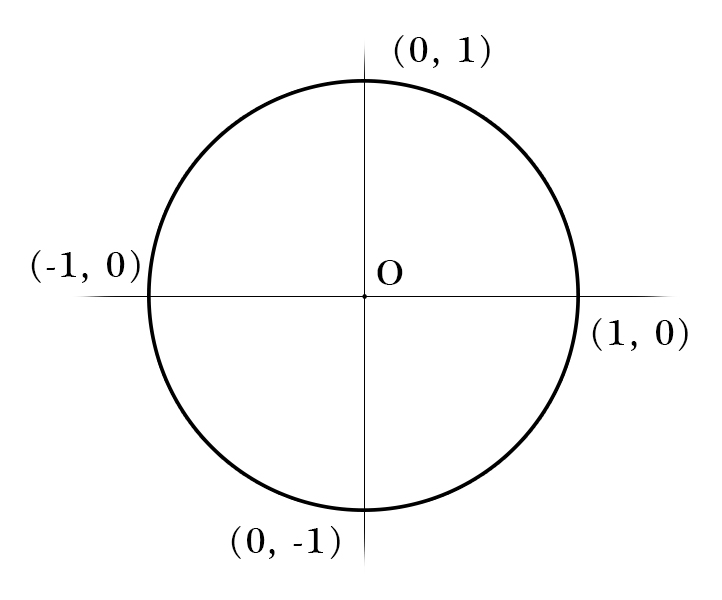
Rappresenta il luogo dei punti che hanno la stessa distanza dall'origine, in formule $$ (x,y)|x^2+y^2=1 $$ Consideriamo adesso una retta parallela all'asse y e passante per l'asse x, cioè tutti i punti $$ (x,y)|x=1 $$
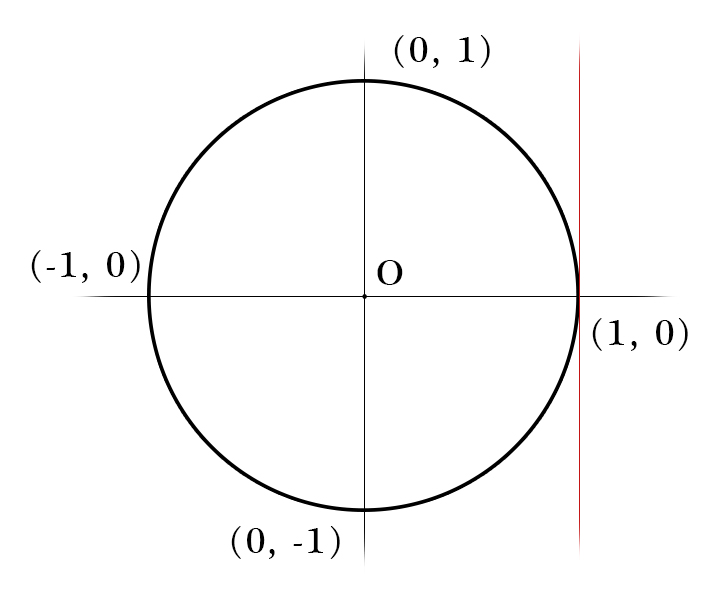
Vogliamo individuare la posizione di un punto P che si trova sul cerchio, e per fare ciò è sufficiente conoscere le sue due coordinate x e y $$ P=(x,y) $$

---

Per trovare la posizione di un punto, in maniera non ambigua, si può utilizzare il concetto di angolo. Un angolo è un rapporto di lunghezze.
Per convenzione prendiamo nel punto (1,0) un angolo pari a 0. L'angolo (misurato in radianti) si trova dividendo l'arco di cerchio S per il raggio R
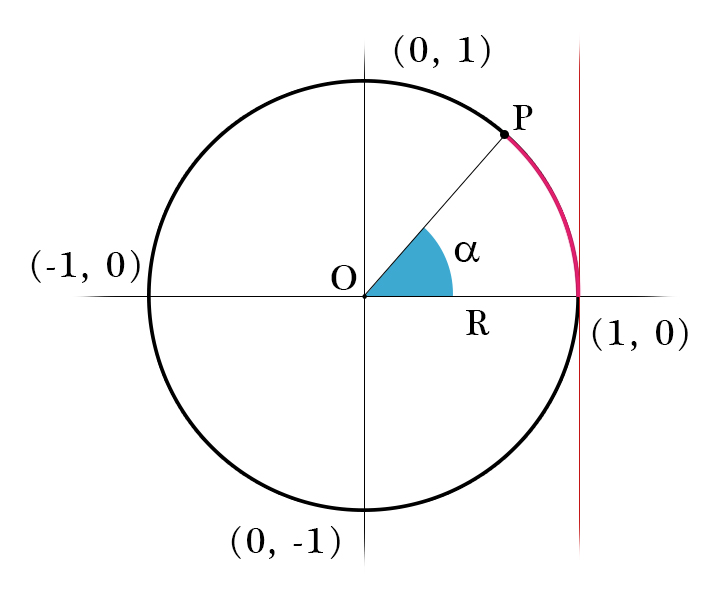
$$ \alpha =\frac{S}{R} $$ La circonferenza del cerchio è $$ S=2\pi\cdot R $$ Dove \(2\pi\) è l'angolo giro in radianti.
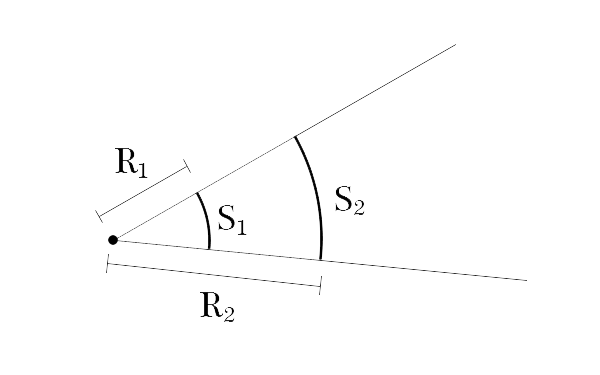
Come si passa da radianti a gradi? Un grado è la 360 esima parte di un angolo giro, in formule $$ 360^{\circ}=2\pi $$ Dividiamo tutto per 2, otteniamo $$ 180^{\circ}=\pi $$ Dai cui $$ 1 rad=\frac{180}{\pi} $$

---

Prima di dare la definizione di tangente, bisogna passare per la "trigonometria dei triangoli rettangoli". Un triangolo si dice rettangolo quando i due cateti formano un angolo retto, cioè \(90^{\circ}\), come mostrato in figura
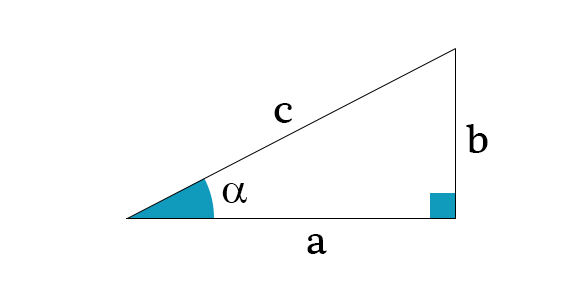
Se conosciamo l'ipotenusa c e l'angolo \(\alpha\), possiamo determinare i cateti a e b, utilizzando le seguenti formule $$ a=c\cdot cos\alpha $$ $$ b=c\cdot sin\alpha $$ Consideriamo la seguente figura
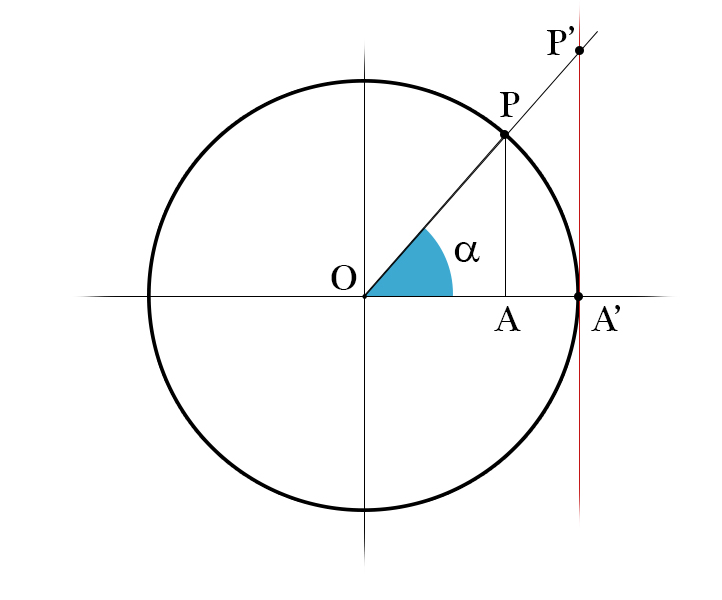
La tangente di \(\alpha\) è la coordinata y del punto \(P'\), che rappresenta l'intersezione tra la semiretta che parte dall'origine del cerchio e passa dal punto \(P\), che ha l'angolo \(\alpha\), e la retta x=1. In sostanza è la lunghezza del segmento \(A'P'\). I triangoli rettangoli \(OAP\) e \(OA'P'\) sono simili, dunque i due cateti \(OA\) e \(AP\) sono proporzionali ai due cateti \(OA'\) e \(A'P'\), con lo stesso rapporto, cioè $$ \frac{AP}{OA}=\frac{A'P'}{OA'} $$ Per le relazioni viste prima di trigonometria dei triangoli rettangoli e per la definizione appena data di tangente, possiamo riscrivere la relazione nel seguente modo $$ \frac{R\cdot sin\alpha}{R\cdot cos\alpha}=\frac{tan\alpha}{R} $$ Per il triangolo \(OAP\) il raggio R rappresenta l'ipotenusa, mentre per \(OA'P'\) rappresenta la coordinata x, cioè la lunghezza del segmento \(OA'\). Considerando che il raggio R è pari a 1, possiamo concludere che $$ \frac{sin\alpha}{cos\alpha}=tan\alpha $$ Il valore della tangente si trova graficamente sfruttando la sua definizione, bisogna sempre cercare l'intersezione con la retta x=1.
Ad esempio quando \(\alpha\) è 0, l'intersezione coincide proprio con 0. Se \(\alpha=\frac{\pi}{2}\) oppure \(\frac{3}{4} \pi\) le due rette non si intersecano mai perchè sono parallele, dunque la tangente non è definita.
Potete tranquillamente divertirvi a trovare alcuni valori di tangente.