Disequazioni logaritmiche
Una disequazione logaritmica è una disequazione dove l'incognita compare all'interno di uno o più logaritmi. Per risolvere questo tipo di disequazioni è necessario conoscere tutto quello che è stato detto per le equazioni logaritmiche. Quello che cambia è che qui abbiamo sistemi di disequazioni da risolvere. Nulla di complesso.
Esempio 1
Risolvere la seguente disequazione logaritmica \( log_2(2x+1)\leq 2 \)
Possiamo applicare l'esponenziale a entrambi i membri, senza dimenticarci delle condizioni di esistenza dei logaritmi. Inoltre visto che la base è maggiore di \(1\) il verso della disequazione rimane invariato, vale lo stesso discorso fatto nelle disequazioni esponenziali $$ \left\{\begin{matrix} 2x+1>0\rightarrow condizione\hspace{3mm} di \hspace{3mm}esistenza \\ 2x+1\leq 2^2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} 2x+1>0\rightarrow C.E. \\ 2x+1\leq 2^2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} 2x+1>0\rightarrow C.E. \\ 2x+1\leq 2^2 \end{matrix}\right. $$ Risolviamo il sistema $$ \left\{\begin{matrix} x>-\frac{1}{2} \\ 2x+1\leq 4\Rightarrow x\leq \frac{3}{2} \end{matrix}\right. $$
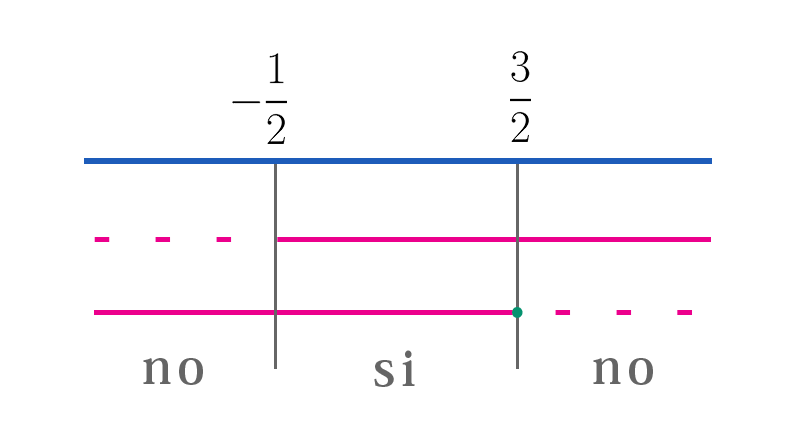
La soluzione del sistema e quindi della disequazione è $$ -\frac{1}{2}< x\leq \frac{3}{2} $$ Attenzione perchè il valore \(\frac{3}{2}\) è soluzione di entrambe le disequazioni del sistema, dunque va inclusa.
Esempio 2
Risolvere la seguente disequazione logaritmica \( log_{\frac{1}{2}}(x+2)< 0 \)
Scriviamo il solito sistema, con l'accortezza che stavolta il verso va cambiato in quanto la base è minore di \(1\) $$ \left\{\begin{matrix} x+2>0 \Rightarrow x> -2\\ x+2> \left(\frac{1}{2}\right)^0 \Rightarrow x> -1 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x+2>0 \Rightarrow x> -2\\ x+2> \left(\frac{1}{2}\right)^0 \Rightarrow x> -1 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x+2>0 \Rightarrow x> -2\\ x+2> \left(\frac{1}{2}\right)^0 \Rightarrow x> -1 \end{matrix}\right. $$
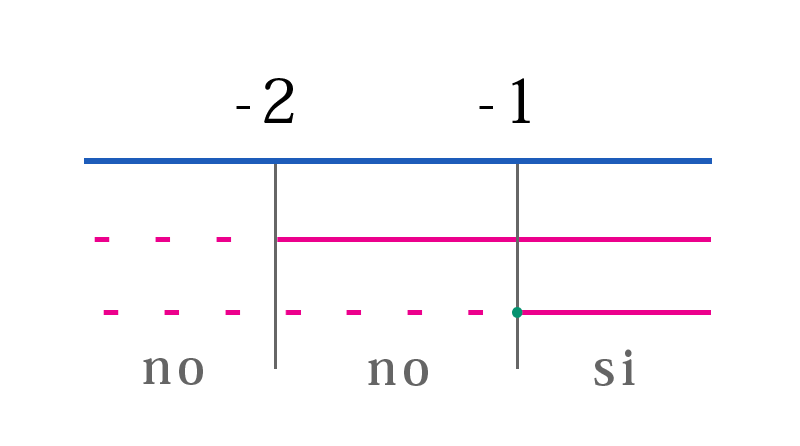
La soluzione della disequazione è $$ x> -1 $$
Esempio 3
Risolvere la seguente disequazione logaritmica \( log_2(x-3)> log_2(x+2) \) \( log_2(x-3)> log_2(x+2) \) \( log_2(x-3)> log_2(x+2) \)
E' possibile eliminare direttamente i logaritmi in quanto stessa base. Se le basi sono diverse basta fare un cambio di base. Scriviamo il sistema di disequazioni con le condizioni di esistenza $$ \left\{\begin{matrix} x-3>0 \Rightarrow x> 3\\ x+2> 0 \Rightarrow x> -2 \\ x-3> x+2 \Rightarrow -3>2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x-3>0 \Rightarrow x> 3\\ x+2> 0 \Rightarrow x> -2 \\ x-3> x+2 \Rightarrow -3>2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x-3>0 \Rightarrow x> 3\\ x+2> 0 \Rightarrow x> -2 \\ x-3> x+2 \Rightarrow -3>2 \end{matrix}\right. $$ La terza disequazione è impossibile in quanto \(-3\) non è maggiore di \(2\). Dunque il sistema è impossibile e la disequazione di partenza non ha nessuna soluzione.
La cosa fondamentale di questa tipologia di disequazioni è ricondursi ad una delle forme elementari, utilizzando proprietà dei logaritmi, cambiamento di base e cambio di variabile.
Esempio 1Risolvere la seguente disequazione logaritmica \( log_2(2x+1)\leq 2 \)
Possiamo applicare l'esponenziale a entrambi i membri, senza dimenticarci delle condizioni di esistenza dei logaritmi. Inoltre visto che la base è maggiore di \(1\) il verso della disequazione rimane invariato, vale lo stesso discorso fatto nelle disequazioni esponenziali $$ \left\{\begin{matrix} 2x+1>0\rightarrow condizione\hspace{3mm} di \hspace{3mm}esistenza \\ 2x+1\leq 2^2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} 2x+1>0\rightarrow C.E. \\ 2x+1\leq 2^2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} 2x+1>0\rightarrow C.E. \\ 2x+1\leq 2^2 \end{matrix}\right. $$ Risolviamo il sistema $$ \left\{\begin{matrix} x>-\frac{1}{2} \\ 2x+1\leq 4\Rightarrow x\leq \frac{3}{2} \end{matrix}\right. $$
La soluzione del sistema e quindi della disequazione è $$ -\frac{1}{2}< x\leq \frac{3}{2} $$ Attenzione perchè il valore \(\frac{3}{2}\) è soluzione di entrambe le disequazioni del sistema, dunque va inclusa.
Esempio 2Risolvere la seguente disequazione logaritmica \( log_{\frac{1}{2}}(x+2)< 0 \)
Scriviamo il solito sistema, con l'accortezza che stavolta il verso va cambiato in quanto la base è minore di \(1\) $$ \left\{\begin{matrix} x+2>0 \Rightarrow x> -2\\ x+2> \left(\frac{1}{2}\right)^0 \Rightarrow x> -1 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x+2>0 \Rightarrow x> -2\\ x+2> \left(\frac{1}{2}\right)^0 \Rightarrow x> -1 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x+2>0 \Rightarrow x> -2\\ x+2> \left(\frac{1}{2}\right)^0 \Rightarrow x> -1 \end{matrix}\right. $$
La soluzione della disequazione è $$ x> -1 $$
Esempio 3Risolvere la seguente disequazione logaritmica \( log_2(x-3)> log_2(x+2) \) \( log_2(x-3)> log_2(x+2) \) \( log_2(x-3)> log_2(x+2) \)
E' possibile eliminare direttamente i logaritmi in quanto stessa base. Se le basi sono diverse basta fare un cambio di base. Scriviamo il sistema di disequazioni con le condizioni di esistenza $$ \left\{\begin{matrix} x-3>0 \Rightarrow x> 3\\ x+2> 0 \Rightarrow x> -2 \\ x-3> x+2 \Rightarrow -3>2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x-3>0 \Rightarrow x> 3\\ x+2> 0 \Rightarrow x> -2 \\ x-3> x+2 \Rightarrow -3>2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x-3>0 \Rightarrow x> 3\\ x+2> 0 \Rightarrow x> -2 \\ x-3> x+2 \Rightarrow -3>2 \end{matrix}\right. $$ La terza disequazione è impossibile in quanto \(-3\) non è maggiore di \(2\). Dunque il sistema è impossibile e la disequazione di partenza non ha nessuna soluzione.
Esercizi di Matematica
Film Matematici
Formulari di Matematica
Calcolatori Matematici
Ebook
Paradossi
Podcast
