Sistemi di disequazioni
Un sistema di disequazioni è un insieme di disequazioni che devono valere contemporaneamente. In questo sistema possiamo avere sia disequazioni di primo grado e sia disequazioni di secondo grado.
Per risolvere un sistema di questo tipo è sufficiente risolvere le disequazioni singolarmente per poi combinare le soluzioni in un unico grafico, in modo da verificare se esistono soluzioni in comune tra tutte le disequazioni.
Esempio 1
Risolvere il seguente sistema di disequazioni \( \left\{\begin{matrix} x+2<{4} \\ -2x+1>0 \end{matrix}\right. \)
Risolviamo singolarmente le due disequazioni $$ x+2<{4}\Rightarrow x<{4-2}\Rightarrow x<{2} $$ $$ x+2<{4}\Rightarrow x<{4-2}\Rightarrow x<{2} $$ $$ x+2<{4}\Rightarrow x<{4-2}\Rightarrow x<{2} $$ $$ -2x+1>0\Rightarrow -2x>-1\Rightarrow 2x<{1}\Rightarrow x<{\frac{1}{2}} $$ $$ -2x+1>0\Rightarrow -2x>-1\Rightarrow 2x<{1} $$ $$ \Downarrow $$ $$ x<{\frac{1}{2}} $$ $$ -2x+1>0\Rightarrow -2x>-1 $$ $$ \Downarrow $$ $$ 2x<{1} $$ $$ \Downarrow $$ $$ x<{\frac{1}{2}} $$ Inseriamo in un unico grafico le soluzioni delle due disequazioni
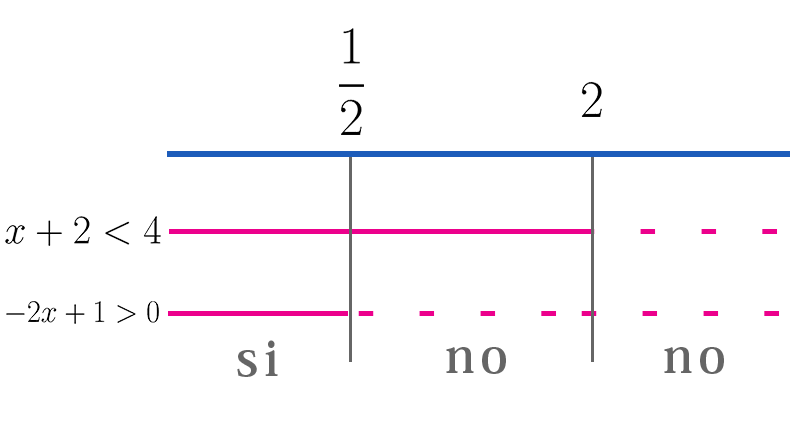
Il sistema è verificato a sinistra di \(\frac{1}{2}\), cioè $$ x\in (-\infty,\frac{1}{2}) $$
Esempio 2
Risolvere il seguente sistema di disequazioni \( \left\{\begin{matrix} x^2+3x+2<{0} \\ x-2<{0} \\ x+1\geq 0 \end{matrix}\right. \)
Risolviamo singolarmente le due disequazioni. Calcoliamo il determinante e le soluzioni dell'equazione associata alla prima disequazione $$ \Delta=9-8=1 $$ $$ x_1=\frac{-3+1}{2}=-1 $$ $$ x_2=\frac{-3-1}{2}=-2 $$ Visto che il verso è di minore, la disequazione è verificata per valori interni, cioè $$ x\in (-2,-1) $$ Risolviamo adesso le altre due disequazioni di primo grado $$ x-2<{0}\Rightarrow x<{2} $$ $$ x+1\geq 0\Rightarrow x\geq -1 $$ Inseriamo in un unico grafico le soluzioni delle tre disequazioni
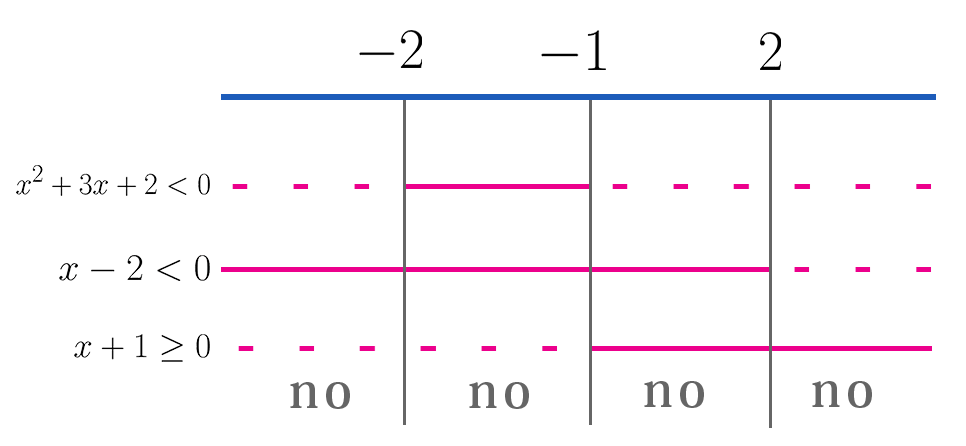
Potete notare anche da voi che non esiste un intervallo dove sono verificate tutte e tre le disequazioni. Questo significa che il sistema non ha nessuna soluzione.
Per risolvere un sistema di questo tipo è sufficiente risolvere le disequazioni singolarmente per poi combinare le soluzioni in un unico grafico, in modo da verificare se esistono soluzioni in comune tra tutte le disequazioni.
Esempio 1Risolvere il seguente sistema di disequazioni \( \left\{\begin{matrix} x+2<{4} \\ -2x+1>0 \end{matrix}\right. \)
Risolviamo singolarmente le due disequazioni $$ x+2<{4}\Rightarrow x<{4-2}\Rightarrow x<{2} $$ $$ x+2<{4}\Rightarrow x<{4-2}\Rightarrow x<{2} $$ $$ x+2<{4}\Rightarrow x<{4-2}\Rightarrow x<{2} $$ $$ -2x+1>0\Rightarrow -2x>-1\Rightarrow 2x<{1}\Rightarrow x<{\frac{1}{2}} $$ $$ -2x+1>0\Rightarrow -2x>-1\Rightarrow 2x<{1} $$ $$ \Downarrow $$ $$ x<{\frac{1}{2}} $$ $$ -2x+1>0\Rightarrow -2x>-1 $$ $$ \Downarrow $$ $$ 2x<{1} $$ $$ \Downarrow $$ $$ x<{\frac{1}{2}} $$ Inseriamo in un unico grafico le soluzioni delle due disequazioni
Il sistema è verificato a sinistra di \(\frac{1}{2}\), cioè $$ x\in (-\infty,\frac{1}{2}) $$
Esempio 2Risolvere il seguente sistema di disequazioni \( \left\{\begin{matrix} x^2+3x+2<{0} \\ x-2<{0} \\ x+1\geq 0 \end{matrix}\right. \)
Risolviamo singolarmente le due disequazioni. Calcoliamo il determinante e le soluzioni dell'equazione associata alla prima disequazione $$ \Delta=9-8=1 $$ $$ x_1=\frac{-3+1}{2}=-1 $$ $$ x_2=\frac{-3-1}{2}=-2 $$ Visto che il verso è di minore, la disequazione è verificata per valori interni, cioè $$ x\in (-2,-1) $$ Risolviamo adesso le altre due disequazioni di primo grado $$ x-2<{0}\Rightarrow x<{2} $$ $$ x+1\geq 0\Rightarrow x\geq -1 $$ Inseriamo in un unico grafico le soluzioni delle tre disequazioni
Potete notare anche da voi che non esiste un intervallo dove sono verificate tutte e tre le disequazioni. Questo significa che il sistema non ha nessuna soluzione.
Esercizi di Matematica
Film Matematici
Formulari di Matematica
Calcolatori Matematici
Ebook
Paradossi
Podcast
