Una disequazione è una disuguaglianza tra due termini. Si presenta come una equazione solo che al posto del simbolo di uguale possiamo trovare sostanzialmente quattro simboli:

• Maggiore >;
• Minore < ;
• Maggiore o uguale \(\geq\);
• Minore o uguale \(\leq\) .

Una disequazione, a differenza delle equazioni, è verificata per un certo intervallo di valori.
Valgono i principi di equivalenza che abbiamo visto per le equazioni, con una proprietà molto importante che è la seguente
Una disequazione di primo grado è una disequazione dove l'incognita compare con grado massimo pari ad uno. Ad esempio $$ x-1>0 $$ Per risolvere una disequazione di primo grado è sufficiente utilizzare gli stessi metodi che abbiamo visto per le equazioni di primo grado.

---

Una disequazione di secondo grado è una disequazione dove l'incognita compare con grado massimo pari a due. Questo tipo di disequazioni si possono presentare sotto varie forme, quella completa è la seguente $$ ax^2+bx+c\gtreqless 0 $$Per comodità considereremo il caso in cui \(a>0\). Se è negativo basterà moltiplicare tutto per \(-1\) e cambiare verso alla disequazione.
Per risolvere questo tipo di disequazioni bisogna analizzare il verso della disequazione e calcolare il \(\Delta\) della equazione di secondo grado associata alla disequazione di partenza. Si possono verificare tre casi:

• CASO 1.1 \(\rightarrow\) \(ax^2+bx+c> 0\) & \(\Delta>0\):
L'equazione ha verso di maggiore e il \(\Delta\) è positivo. In questo caso si procede con il calcolo delle soluzioni della equazione associata e la disequazione è verificata per valori esterni, cioè


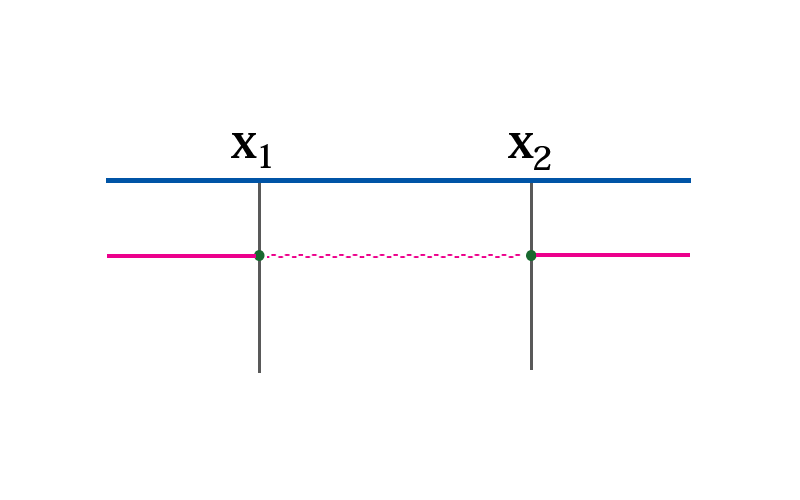
Sotto forma di intervalli possiamo scrivere, supponendo \(x_1<{x_2}\) $$ x\in (-\infty,x_1)\cup (x_2,+\infty) $$ $$ x\in (-\infty,x_1)\cup (x_2,+\infty) $$ $$ x\in (-\infty,x_1)\cup (x_2,+\infty) $$
  Esempio
Risolvere la seguente disequazione di secondo grado \( x^2+5x+6>0 \)
---
Calcoliamo il determinante dell'equazione associata \(x^2+5x+6=0\) $$ \Delta=b^2-4ac $$ $$ \downarrow $$ $$ \Delta=25-24=1 $$ $$ \downarrow $$ $$ \Delta=25-24=1 $$ $$ \downarrow $$ $$ x_{1,2}=\frac{-b\pm \sqrt b^2-4ac}{2a} $$ $$ x_{1,2}=\frac{-b\pm \sqrt b^2-4ac}{2a} $$ $$ x_{1,2}=\frac{-b\pm \sqrt b^2-4ac}{2a} $$ $$ \downarrow $$ $$ x_{1,2}=\frac{-5\pm \sqrt 1}{2} $$ $$ \downarrow $$ $$ x_{1}=\frac{-5+1}{2}=-2 $$ $$ x_{2}=\frac{-5-1}{2}=-3 $$ Visto che il verso è di maggiore e il \(\Delta\) è positivo, la disequazione è verificata per valori esterni, cioè


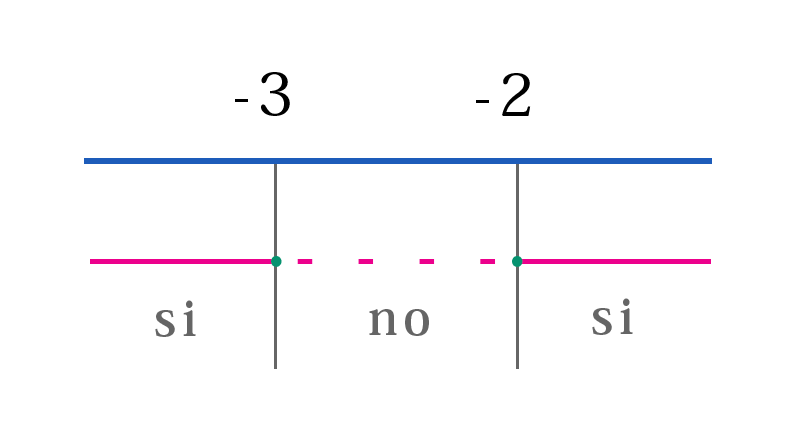
$$ x\in (-\infty,-3)\cup(-2,+\infty) $$ $$ x\in (-\infty,-3)\cup(-2,+\infty) $$ $$ x\in (-\infty,-3)\cup(-2,+\infty) $$
• CASO 1.2 \(\rightarrow\) \(ax^2+bx+c< 0\) & \(\Delta>0\):
L'equazione ha verso di minore e il \(\Delta\) è positivo. In questo caso si procede con il calcolo delle soluzioni della equazione associata e la disequazione è verificata per valori interni, cioè


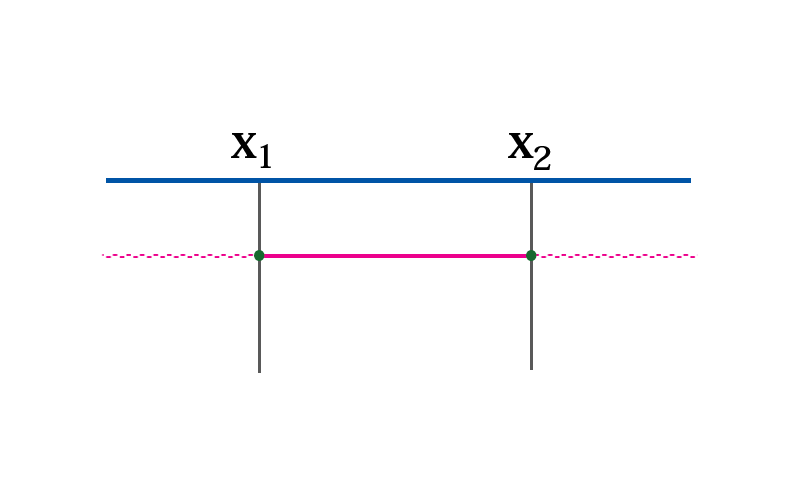
Sotto forma di intervalli possiamo scrivere, supponendo \(x_1<{x_2}\) $$ x\in (x_1,x_2) $$
  Esempio
Risolvere la seguente disequazione di secondo grado \( x^2+5x+6\leq 0 \)
---
Il determinante e le soluzioni della equazione associata li abbiamo trovati nell'esempio precedente, dunque $$ x_{1}=\frac{-5+1}{2}=-2 $$ $$ x_{2}=\frac{-5-1}{2}=-3 $$ Visto che il verso è di minore e il \(\Delta\) è positivo, la disequazione è verificata per valori interni inclusi gli estremi perchè c'è anche il segno di uguale, cioè


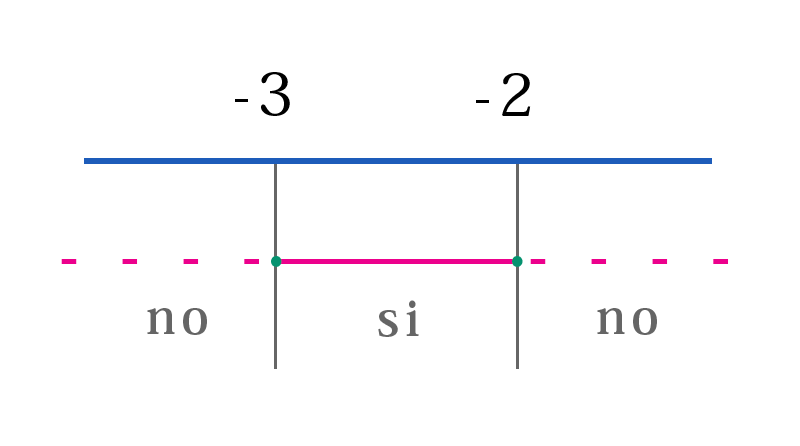
$$ x\in [-3,-2] $$

• CASO 2.1 \(\rightarrow\) \(ax^2+bx+c> 0\) & \(\Delta=0\):
L'equazione ha verso di maggiore e il \(\Delta\) è nullo. In questo caso si tratta di quadrato di binomio, si procede con il calcolo della soluzione della equazione associata e la disequazione è verificata per tutti i valori di \(\mathbb{R}\) tranne il valore della soluzione dell'equazione, cioè


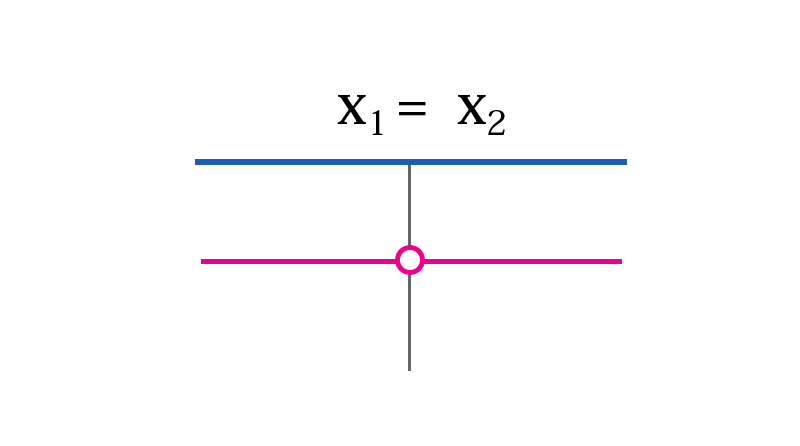
Sotto forma di intervalli possiamo scrivere, visto che \(x_1=x_2\) $$ x\in \mathbb{R}\setminus\{x_1\} $$
  Esempio
Risolvere la seguente disequazione di secondo grado \( -x^2+4x-4<{0} \)
---
Per prima cosa conviene cambiare tutto di segno in modo da avere il coefficiente \(a\) positivo, invertendo anche il verso della disequazione $$ x^2-4x+4>{0} $$ Calcoliamo il determinante e le due soluzioni dell'equazione associata $$ \Delta=16-16=0 $$ $$ x_{1}=x_{2}=\frac{4+0}{2}=2 $$ $$ x_{1}=x_{2}=\frac{4+0}{2}=2 $$ $$ x_{1}=x_{2}=\frac{4+0}{2}=2 $$ Visto che il verso è di maggiore e il \(\Delta\) è nullo, la disequazione è verificata per valori di \(\mathbb{R}\) escluso il \(2\) perchè è la radice dell'equazione, cioè


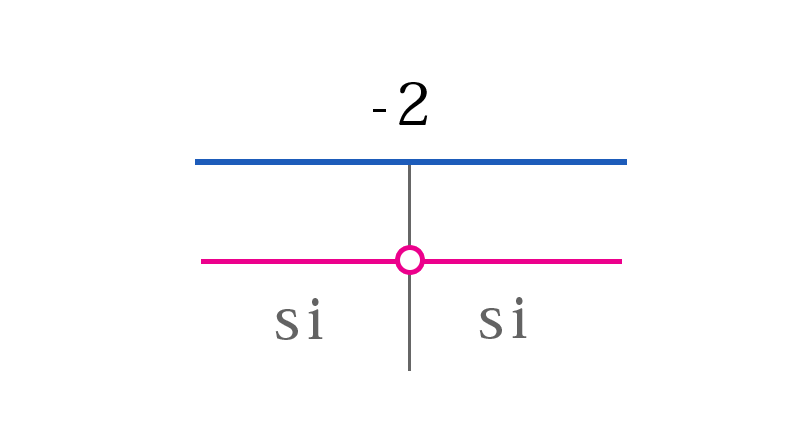
$$ x\in \mathbb{R}\setminus\{2\} $$
• CASO 2.2 \(\rightarrow\) \(ax^2+bx+c< 0\) & \(\Delta=0\):
L'equazione ha verso di minore e il \(\Delta\) è nullo. In questo caso si tratta di quadrato di binomio, dunque non può mai essere negativo, Non abbiamo alcun intervallo di soluzione , cioè

  Esempio
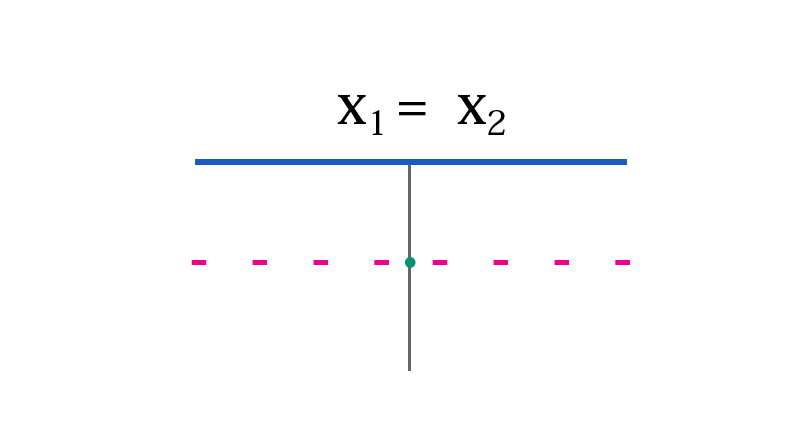
Risolvere la seguente disequazione di secondo grado \( x^2-4x+4\leq{0} \)
---
Abbiamo già visto prima che si tratta di un quadrato di binomio, dunque visto che il \(\Delta\) è nullo e il verso è di minore o uguale, in teoria non dovrebbe avere alcuna soluzione, in quanto un quadrato non può essere mai negativo. Il problema è che in questo caso esiste anche il segno di uguale, dunque in realtà esiste una soluzione di questa disequazione che coincide con il valore che annulla il polinomio associato all'equazione, cioè


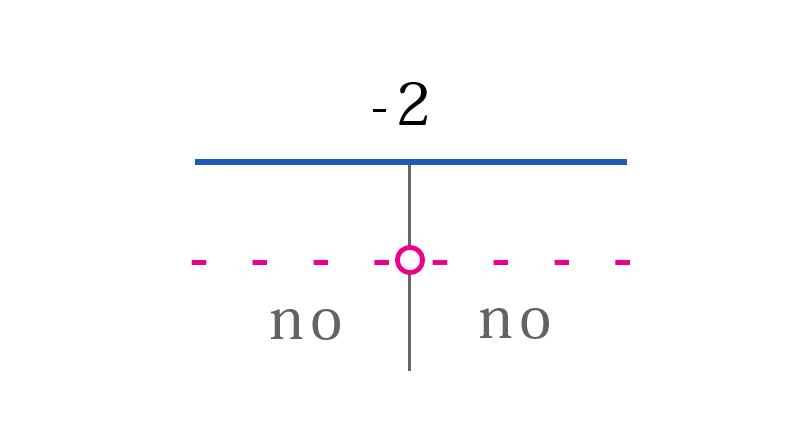
In termini di intervallo la soluzione è dunque $$ x=2 $$

• CASO 3.1 \(\rightarrow\) \(ax^2+bx+c> 0\) & \(\Delta<{0}\):
L'equazione ha verso di maggiore e il \(\Delta\) è negativo. In questo caso non dobbiamo calcolare alcuna soluzione dell'equazione associata. In particolare la disequazione è verificata per tutti i valori di \mathbb{R}.
Sotto forma di intervalli possiamo scrivere $$ x\in \mathbb{R} $$
  Esempio
Risolvere la seguente disequazione di secondo grado \( x^2+2x+2>{0} \)
---
Il determinante è negativo. Visto che il segno è di maggiore la disequazione è vericata in tutto \(\mathbb{R}\) $$ x\in \mathbb{R} $$
• CASO 3.2 \(\rightarrow\) \(ax^2+bx+c< 0\) & \(\Delta<{0}\):
L'equazione ha verso di minore e il \(\Delta\) è negativo. In questo caso non dobbiamo calcolare alcuna soluzione dell'equazione associata. In particolare la disequazione non è mai verificata.
  Esempio
Risolvere la seguente disequazione di secondo grado \( x^2+2x+2\leq{0} \)
---
Il determinante è negativo. Visto che il segno è di minore o uguale la disequazione non ha alcuna soluzione. Anche se è presente il segno di uguale, ricordiamo che non esiste una soluzione in \(\mathbb{R}\).