Fino ad adesso abbiamo visto che il vettore posizione di un punto materiale può cambiare nel tempo, dando origine a quella che abbiamo definito velocità. Quest'ultima può cambiare nel tempo, possiamo andare più veloci oppure più lenti. Nella nostra vita quotidiana abbiamo a che fare con il concetto di accelerazione, ad esempio nelle auto è presente il pedale che ci permette di accelerare, cioè di aumentare la velocità dell'auto.
Consideriamo un punto materiale che cambia la sua velocità nel tempo
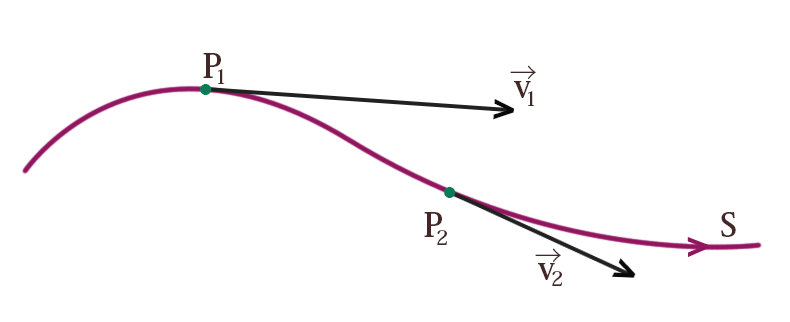
L'accelerazione è semplicemente la variazione della velocità nel tempo $$ \vec{a}_m=\frac{\Delta \vec{v}}{\Delta t} $$ Quando trovate un \(\Delta\) ci stiamo riferendo ad una variazione della grandezza che segue il simbolo di \(\Delta\), finale meno iniziale. All'istante \(t_1\) il corpo avrà \(\vec{v}(t_1)\) . All'istante \(t_2\) il corpo avrà \(\vec{v}(t_2)\), dunque $$ \Delta \vec{v}=\vec{v}(t_2)-\vec{v}(t_1) $$ $$ \Delta t=t_2-t_1 $$ $$ \vec{a}_m=\frac{\vec{v}(t_2)-\vec{v}(t_1)}{t_2-t_1} $$ Questa in realtà si chiama accelerazione media, perchè rappresenta una media, in quanto il \(\Delta t\) è un intervallo temporale ampio. Non abbiamo informazioni sulla accelerazione in un certo istante, abbiamo solo quella nell'intervallo. Abbiamo già visto che l'accelerazione ha le dimensioni di una lunghezza su un tempo al quadrato $$ [v]=[L][t^{-2}] $$ Nel sistema internazionale l'accelerazione si misura in metri al secondo al quadrato \(\frac{m}{s^2}\).