Legge oraria
Abbiamo visto che l'equazione della traiettoria si ricava facilmente dai moti componenti. Ma come si trova invece la legge oraria?
Consideriamo un corpo che si sposta lungo la traiettoria di una quantità \(\Delta s\). Questa quantità può essere scomposta in uno spostamento orizzontale \(\Delta x\) e in uno verticale \(\Delta y\)
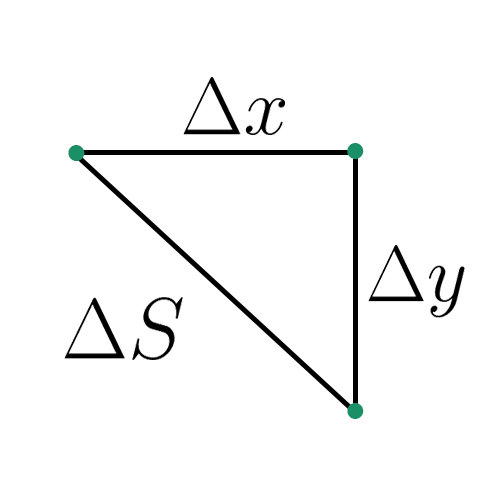
Dal teorema di Pitagora, essendo un triangolo rettangolo, troviamo la seguente relazione $$ \Delta s=\sqrt{\Delta x^2+\Delta y^2} $$ In questa relazione manca il tempo \(\Delta t\) impiegato dal corpo per percorrere il tratto \(\Delta s\). Moltiplichiamo e dividiamo tutto per \(\Delta t\) $$ \Delta s=\sqrt{\Delta x^2+\Delta y^2}\frac{\Delta t}{\Delta t} $$ Portiamo \(\frac{1}{\Delta t}\) dentro il segno di radice $$ \Delta s=\sqrt{\frac{\Delta x^2+\Delta y^2}{\Delta t^2}}\Delta t $$ Spezziamo in due la frazione $$ \Delta s=\sqrt{(\frac{\Delta x}{\Delta t})^2+(\frac{\Delta y}{\Delta t})^2}\Delta t $$ Tutta la curva che rappresenta la traiettoria può essere divisa in tanti spostamenti \(\Delta s\)
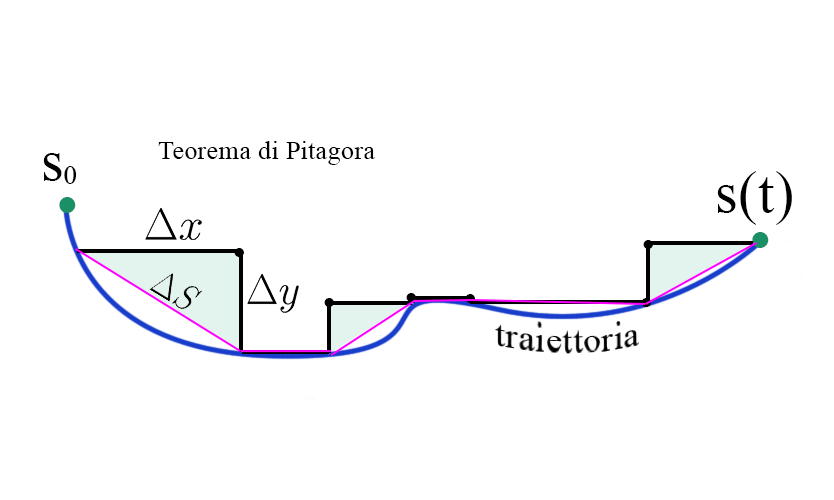
La traiettoria deve essere spezzata in pezzi piccolini per seguire bene la curva e per fare questo dobbiamo ridurre \(\Delta t\) a \(dt\) che è un tempo infinitesimo, in questo modo anche lo spostamento diventa infinitesimo, dunque $$ ds=\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ Visto che dobbiamo coprire tutta la curva, bisogna sommare tutti i pezzetti infinitesimi di spostamento, dunque va fatto l'integrale $$ \int_{s_0}^{s(t)}{ds}=\int_{t_0}^{t}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ $$ \int_{s_0}^{s(t)}{ds}=\int_{t_0}^{t}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ $$ \int_{s_0}^{s(t)}{ds}=\int_{t_0}^{t}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ Questa è la legge oraria che dipende dalle derivate dei moti componenti.
Consideriamo un corpo che si sposta lungo la traiettoria di una quantità \(\Delta s\). Questa quantità può essere scomposta in uno spostamento orizzontale \(\Delta x\) e in uno verticale \(\Delta y\)
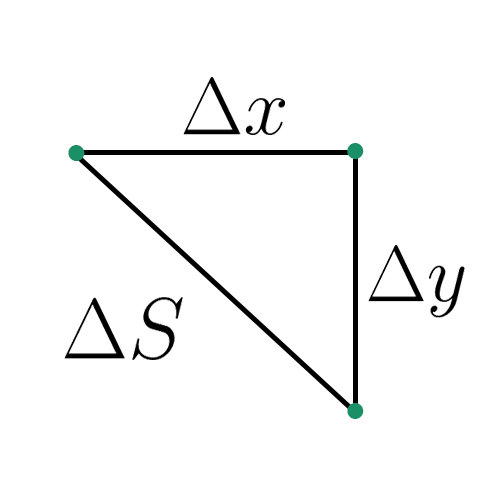
Dal teorema di Pitagora, essendo un triangolo rettangolo, troviamo la seguente relazione $$ \Delta s=\sqrt{\Delta x^2+\Delta y^2} $$ In questa relazione manca il tempo \(\Delta t\) impiegato dal corpo per percorrere il tratto \(\Delta s\). Moltiplichiamo e dividiamo tutto per \(\Delta t\) $$ \Delta s=\sqrt{\Delta x^2+\Delta y^2}\frac{\Delta t}{\Delta t} $$ Portiamo \(\frac{1}{\Delta t}\) dentro il segno di radice $$ \Delta s=\sqrt{\frac{\Delta x^2+\Delta y^2}{\Delta t^2}}\Delta t $$ Spezziamo in due la frazione $$ \Delta s=\sqrt{(\frac{\Delta x}{\Delta t})^2+(\frac{\Delta y}{\Delta t})^2}\Delta t $$ Tutta la curva che rappresenta la traiettoria può essere divisa in tanti spostamenti \(\Delta s\)

La traiettoria deve essere spezzata in pezzi piccolini per seguire bene la curva e per fare questo dobbiamo ridurre \(\Delta t\) a \(dt\) che è un tempo infinitesimo, in questo modo anche lo spostamento diventa infinitesimo, dunque $$ ds=\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ Visto che dobbiamo coprire tutta la curva, bisogna sommare tutti i pezzetti infinitesimi di spostamento, dunque va fatto l'integrale $$ \int_{s_0}^{s(t)}{ds}=\int_{t_0}^{t}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ $$ \int_{s_0}^{s(t)}{ds}=\int_{t_0}^{t}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ $$ \int_{s_0}^{s(t)}{ds}=\int_{t_0}^{t}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt $$ Questa è la legge oraria che dipende dalle derivate dei moti componenti.







