Moti componenti
Consideriamo un punto materiale P e un sistema di assi cartesiani. Questo punto P avrà delle coordinate che dipendono dalle scale utilizzate per gli assi. Colleghiamo l'origine degli assi con il nostro punto P
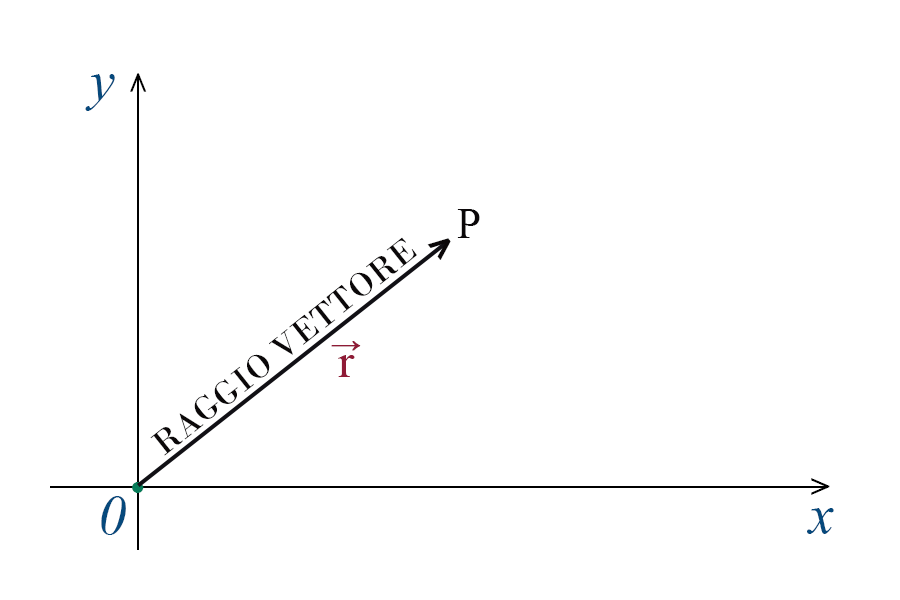
Il vettore \(\vec{r}\) si chiama raggio vettore o vettore posizione. Rappresenta un vettore che parte dall'origine e arriva al punto P, per capirne la posizione.
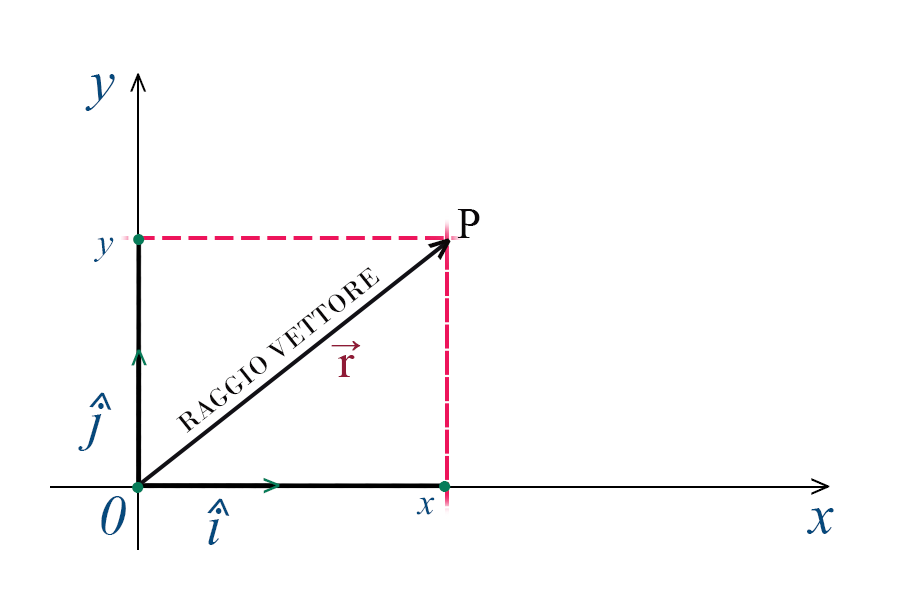
Il vettore \(\vec{r}\), come qualsiasi altro vettore posizionato in un sistema di assi cartesiani, ha le componenti x e y. Per scomporre il vettore però bisogna usare i versori degli assi perchè le componenti prese da sole sono scalari. Utilizzando la regola del parallelogrammo, il vettore lo possiamo scrivere $$ \vec{r}=x\widehat{i}+y\widehat{j} $$
Se ci troviamo nello spazio bisogna aggiungere anche la terza dimensione, quindi la componente z. Quando il corpo si muove anche il vettore \(\vec{r}\) seguirà lo spostamento, dunque cambia nel tempo. In questo modo anche le sue componenti x e y cambiano nel tempo $$ \vec{r(t)}=x(t)\widehat{i}+y(t)\widehat{j} $$
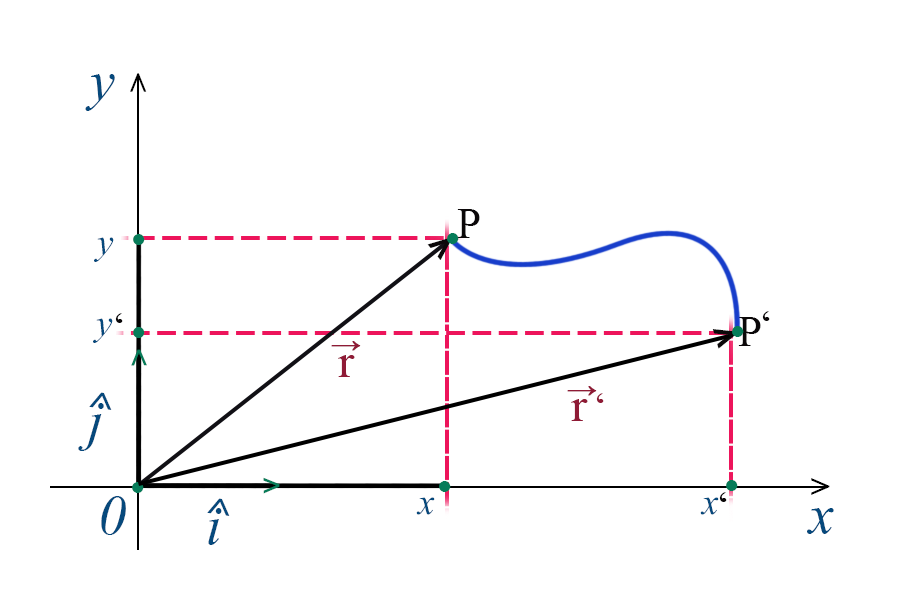
Tali componenti si chiamano moti componenti, che rappresentano,se ci troviamo nello spazio, tre funzioni del tempo $$ \left\{\begin{matrix} x(t) \\ y(t) \\ z(t) \end{matrix}\right. $$ Conoscendo queste funzioni riusciamo ad individuare il movimento del corpo, il suo moto. Se un corpo si muove nel piano ha solo le componenti x e y e si dice che ha 2 gradi di libertà. Se invece il corpo si muove nello spazio ha libertà massima cioè ha 3 gradi di libertà.
Esiste un'altra possibilità per seguire il moto, cioè usando l'equazione della traiettoria effettuata dal corpo. Ovviamente i due metodi sono equivalenti, portano allo stesso risultato. Dipende dal tipo di problema che stiamo affrontando, in quanto a volte conosciamo già la traiettoria.

Il vettore \(\vec{r}\) si chiama raggio vettore o vettore posizione. Rappresenta un vettore che parte dall'origine e arriva al punto P, per capirne la posizione.
Il vettore \(\vec{r}\), come qualsiasi altro vettore posizionato in un sistema di assi cartesiani, ha le componenti x e y. Per scomporre il vettore però bisogna usare i versori degli assi perchè le componenti prese da sole sono scalari. Utilizzando la regola del parallelogrammo, il vettore lo possiamo scrivere $$ \vec{r}=x\widehat{i}+y\widehat{j} $$

Se ci troviamo nello spazio bisogna aggiungere anche la terza dimensione, quindi la componente z. Quando il corpo si muove anche il vettore \(\vec{r}\) seguirà lo spostamento, dunque cambia nel tempo. In questo modo anche le sue componenti x e y cambiano nel tempo $$ \vec{r(t)}=x(t)\widehat{i}+y(t)\widehat{j} $$

Tali componenti si chiamano moti componenti, che rappresentano,se ci troviamo nello spazio, tre funzioni del tempo $$ \left\{\begin{matrix} x(t) \\ y(t) \\ z(t) \end{matrix}\right. $$ Conoscendo queste funzioni riusciamo ad individuare il movimento del corpo, il suo moto. Se un corpo si muove nel piano ha solo le componenti x e y e si dice che ha 2 gradi di libertà. Se invece il corpo si muove nello spazio ha libertà massima cioè ha 3 gradi di libertà.
Esiste un'altra possibilità per seguire il moto, cioè usando l'equazione della traiettoria effettuata dal corpo. Ovviamente i due metodi sono equivalenti, portano allo stesso risultato. Dipende dal tipo di problema che stiamo affrontando, in quanto a volte conosciamo già la traiettoria.







