Precedentemente abbiamo visto che per seguire il moto di un punto materiale è necessario conoscere i moti componenti. In realtà esiste un metodo alternativo che si riferisce all'equazione della traiettoria.
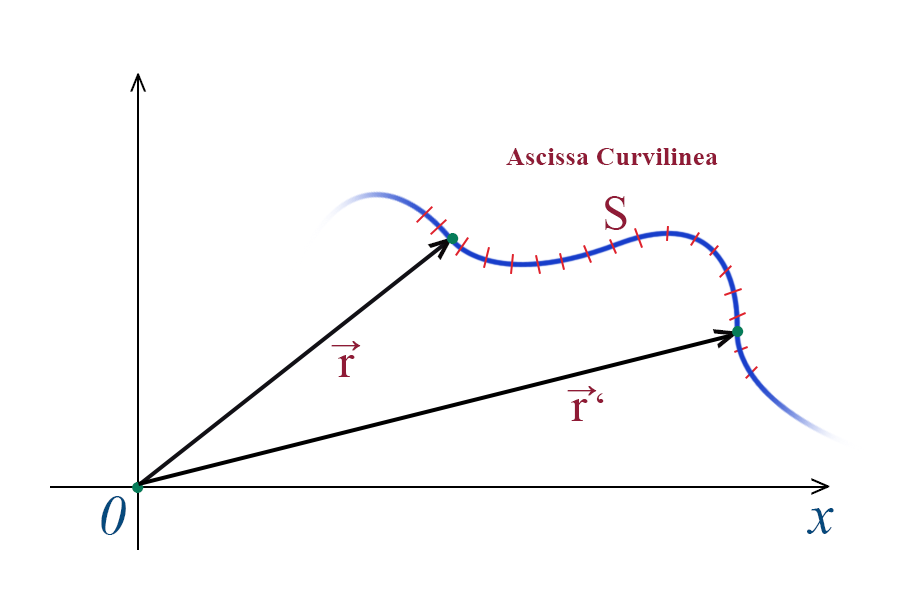
La traiettoria rappresenta una curva che segue il moto del corpo e su di essa possiamo definire una ascissa curvilinea S. Abbiamo in sostanza introdotto un nuovo asse che è rappresentato da una linea curva. Su questo nuovo asse bisogna introdurre una metrica, che ci indica punto per punto dove siamo
L'equazione della traiettoria curvilinea sarà in forma implicita $$ f(x,y)=0 $$ In forma esplicita invece $$ y=f(x) $$ Questa rappresenta una equazione geometrica che ci da informazioni sulla traiettoria, dunque non abbiamo informazioni sul moto del corpo in quanto la variabile tempo è scomparsa. E' necessario aggiungere a questa un'altra equazione, questa volta dipendente dal tempo, che si chiama legge oraria.
La legge oraria ci dice come varia lo spazio percorso in funzione del tempo sulla traiettoria e si indica con \(S(t)\). Questo approccio è equivalente a quello dei moti componenti $$ \left\{\begin{matrix} x(t) \\ y(t) \\ \end{matrix}\right. \Rightarrow \left\{\begin{matrix} f(x,y)=0 \\ S(t) \end{matrix}\right. $$ Se siamo nello spazio la legge oraria non cambia perchè ci fornisce sempre la stessa informazione, quella che cambia è l'equazione della traiettoria. Nel piano è una curva nel piano è una superficie, nello spazio è l'intersezione di due superfici $$ \left\{\begin{matrix} x(t) \\ y(t) \\ z(t) \end{matrix}\right. \Rightarrow \left\{\begin{matrix} f(x,y,z)=0 \\ g(x,y,z)=0 \\ S(t) \end{matrix}\right. $$ $$ \left\{\begin{matrix} x(t) \\ y(t) \\ z(t) \end{matrix}\right. \Rightarrow \left\{\begin{matrix} f(x,y,z)=0 \\ g(x,y,z)=0 \\ S(t) \end{matrix}\right. $$ $$ \left\{\begin{matrix} x(t) \\ y(t) \\ z(t) \end{matrix}\right. \Rightarrow \left\{\begin{matrix} f(x,y,z)=0 \\ g(x,y,z)=0 \\ S(t) \end{matrix}\right. $$