Derivata di una Funzione
Definizione di derivata
Prendiamo un sistema di assi cartesiani. Costruiamo una funzione e il suo rapporto incrementale , prendendo un punto di partenza \(x_{0}\)
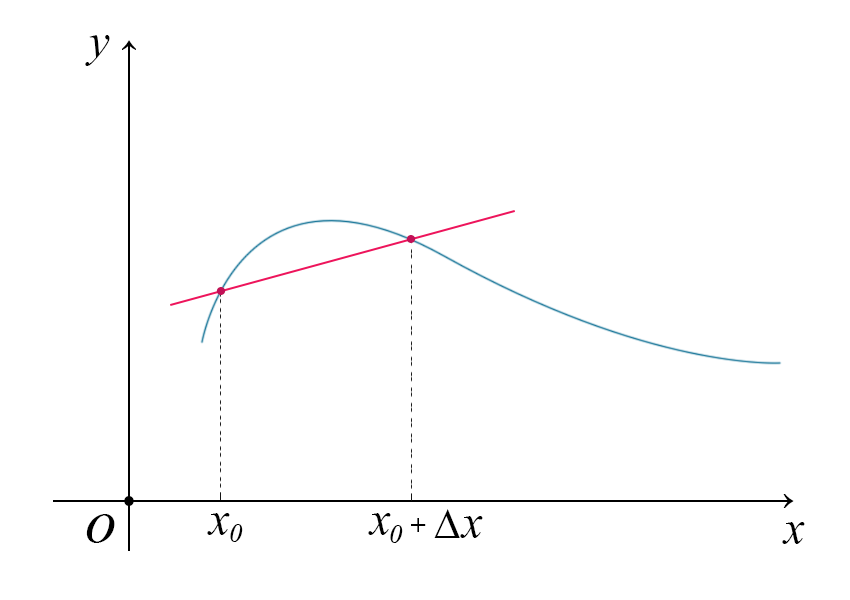
Teniamo ora fermo il punto \(x_{0}\) a variamo \(\Delta x\) . Quello che succede è che la pendenza del segmento che unisce i due punti cambia, come mostrato in figura
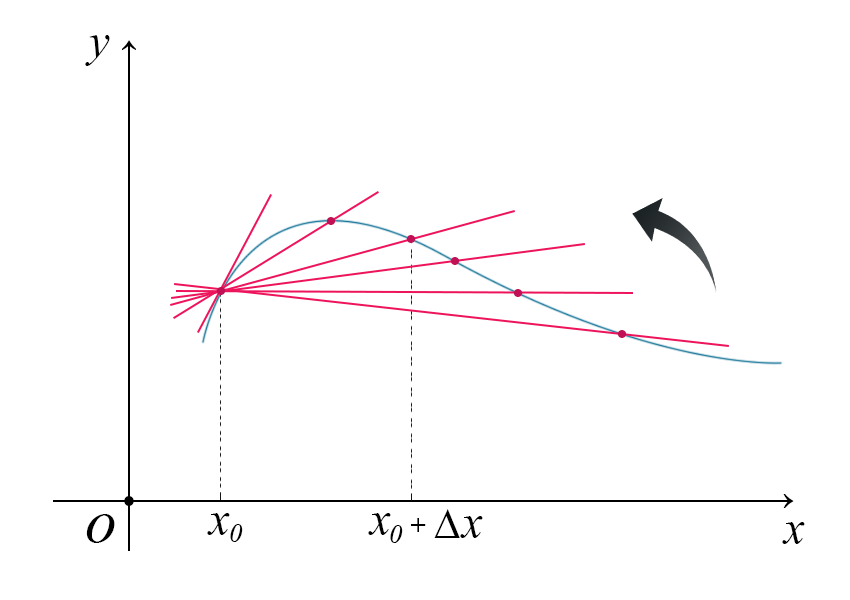
Più \(\Delta x\) dimunuisce, più la pendenza del segmento aumenta, si ha una rotazione intorno al punto \(x_{0}\), finchè non si assesta ad un segmento che coincide con la derivata.
In particolare, quando \(\Delta x\) si avvicina a 0, si ha che il secondo punto \(x_{0}+\Delta x\) tenderà sempre di più ad avvicinarsi a \(x_{0}\), fino a coincidere. In formule $$ \lim_{\Delta x \mapsto 0}\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x} $$ La derivata rappresenta la pendenza della retta tangente alla curva \(f(x)\) nel punto \([x_{0},f(x_{0})]\).
Rappresenta una funzione che dipende dal valore \(x_{0}\) che abbiamo scelto. Si può indicare in diversi modi: $$ f'(x_{0}) $$ $$ \frac{df}{dx}\mid _{x=x_{0}} $$ La seconda scrittura sta ad indicare la derivata della funzione \(f\) rispetto ad \(x\), calcolata nel punto \(x_{0}\). Si può scrivere direttamente $$ \frac{df}{dx} $$ però si perde il riferimento al punto \(x_{0}\).
Vediamo adesso qualche esempio di calcolo della derivata.
Esempio 1Calcoliamo la derivata in x della seguente funzione \(y=f(x)=Ax^2\)
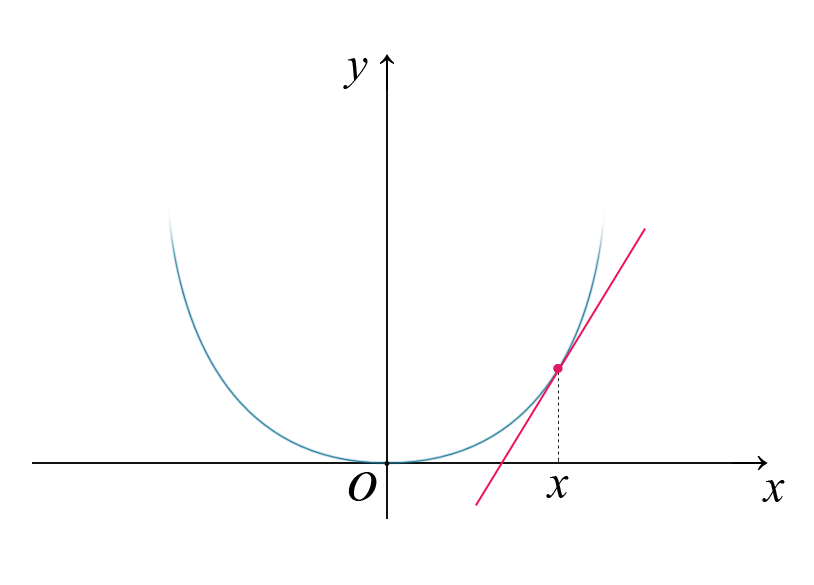
Esempio 2Calcoliamo la derivata in x della seguente funzione \(y=f(x)=Ax^3\)
Calcoliamo per prima cosa il rapporto incrementale $$ \frac{A(x+\Delta x)^3-Ax^3}{\Delta x} $$ $$ A \cdot \left[\frac{x^3+3x^2\Delta x+3x\Delta x^2+\Delta x^3-x^3}{\Delta x}\right]=A3x^2+A3x\Delta x $$ $$ A \cdot \left[\frac{x^3+3x^2\Delta x+3x\Delta x^2+\Delta x^3-x^3}{\Delta x}\right] $$ $$ \Downarrow $$ $$ A3x^2+A3x\Delta x $$ $$ A \cdot \left[\frac{x^3+3x^2\Delta x+3x\Delta x^2+\Delta x^3-x^3}{\Delta x}\right] $$ $$ \Downarrow $$ $$ A3x^2+A3x\Delta x $$ Calcoliamo il limite di questo rapporto incrementale $$ \lim_{\Delta x \mapsto 0}(A3x^2+A3x\Delta x)=A3x^2 $$ $$ \lim_{\Delta x \mapsto 0}(A3x^2+A3x\Delta x)=A3x^2 $$ $$ \lim_{\Delta x \mapsto 0}(A3x^2+A3x\Delta x) $$ $$ \Downarrow $$ $$ A3x^2 $$ Quindi la derivata della funzione \(Ax^3\) si può scrivere come $$ \frac{d}{dx}(Ax^3)=A3x^2 $$ Dove \(\frac{d}{dx}\) si chiama operatore di derivata, il quale unito ad una funzione ne indica la derivata.
Quando \(\Delta x \mapsto 0\), sia \(A3x\Delta x\) che \(A\Delta x^2\) vanno a 0, ma \(\Delta x^2\) si dice essere un infinitesimo di ordine superiore rispetto a \(\Delta x\).
In altri termini \(\Delta x^2\) va più velocemente a 0 rispetto a \(\Delta x\).
Derivate delle funzioni elementari
Calcoliamo la derivata di un paio di funzioni elementari.
InfoCalcoliamo la derivata di \(y=f(x)=A\)
Come al solito partiamo dal calcolo del rapporto incrementale $$ \frac{f(x+\Delta x)-f(x)}{\Delta x} $$ Essendo \(A\) una funzione costante si ha che \(f(x+\Delta x)=A\), dunque $$ \frac{A-A}{\Delta x}=0 $$ Facendo il limite otteniamo sempre 0. Concludiamo che la derivata di una funzione costante è nulla. $$ \frac{dA}{dx}=0 $$
InfoCalcoliamo la derivata di \(y=f(x)=x\)
Calcoliamo il rapporto incrementale $$ \frac{f(x+\Delta x)-f(x)}{\Delta x} $$ $$ \frac{x+\Delta x-x}{\Delta x}=\frac{\Delta x}{\Delta x}=1 $$ $$ \frac{x+\Delta x-x}{\Delta x}=\frac{\Delta x}{\Delta x}=1 $$ $$ \frac{x+\Delta x-x}{\Delta x}=\frac{\Delta x}{\Delta x}=1 $$ Facendo il limite otteniamo sempre 1. Concludiamo che $$ \frac{dx}{dx}=1 $$
InfoCalcoliamo la derivata di \(y=f(x)=sinx\)
Calcoliamo il rapporto incrementale $$ \frac{f(x+\Delta x)-f(x)}{\Delta x} $$ $$ \frac{sin(x+\Delta x)-sinx}{\Delta x} $$ Usando la formula della somma del seno, otteniamo che $$ sin(x+\Delta x)=sinx\cdot cos\Delta x+sin\Delta x\cdot cosx $$ $$ sin(x+\Delta x) $$ $$ \Downarrow $$ $$ sinx\cdot cos\Delta x+sin\Delta x\cdot cosx $$ $$ sin(x+\Delta x) $$ $$ \Downarrow $$ $$ sinx\cdot cos\Delta x+sin\Delta x\cdot cosx $$ Dunque $$ \frac{sinx\cdot cos\Delta x+sin\Delta x\cdot cosx-sinx}{\Delta x} $$ $$ \frac{sinx\cdot cos\Delta x+sin\Delta x\cdot cosx-sinx}{\Delta x} $$ $$ \frac{sinx\cdot cos\Delta x+sin\Delta x\cdot cosx-sinx}{\Delta x} $$ Mettiamo in evidenza \(sinx\) $$ \frac{sinx\cdot( cos\Delta x -1)+sin\Delta x cosx}{\Delta x} $$ $$ \frac{sinx\cdot( cos\Delta x -1)+sin\Delta x cosx}{\Delta x} $$ $$ \frac{sinx\cdot( cos\Delta x -1)+sin\Delta x cosx}{\Delta x} $$ Facciamo il limite $$ \lim_{\Delta x \mapsto 0}\left(\frac{sinx\cdot( cos\Delta x -1)+sin\Delta x cosx}{\Delta x}\right) $$ $$ \lim_{\Delta x \mapsto 0}\left(\frac{sinx\cdot( cos\Delta x -1)+sin\Delta x cosx}{\Delta x}\right) $$ $$ \lim_{\Delta x \mapsto 0}\left(\frac{sinx\cdot( cos\Delta x -1)+sin\Delta x cosx}{\Delta x}\right) $$ Usiamo la proprietà del limite per dividerlo in somma di due limiti $$ \lim_{\Delta x \mapsto 0}\left(\frac{sinx\cdot( cos\Delta x-1)}{\Delta x}\right)+\lim_{\Delta x \mapsto 0}\left(\frac{sin\Delta x cosx}{\Delta x}\right) $$ $$ \lim_{\Delta x \mapsto 0}\left(\frac{sinx\cdot( cos\Delta x-1)}{\Delta x}\right)+ $$ $$ +\lim_{\Delta x \mapsto 0}\left(\frac{sin\Delta x cosx}{\Delta x}\right) $$ $$ \lim_{\Delta x \mapsto 0}\left(\frac{sinx\cdot( cos\Delta x-1)}{\Delta x}\right)+ $$ $$ +\lim_{\Delta x \mapsto 0}\left(\frac{sin\Delta x cosx}{\Delta x}\right) $$ Analizzando i due limiti singolarmente abbiamo che $$ sinx \cdot \lim_{\Delta x \mapsto 0}\left(\frac{( cos\Delta x -1)}{\Delta x}\right)=sinx\cdot0=0 $$ $$ sinx \cdot \lim_{\Delta x \mapsto 0}\left(\frac{( cos\Delta x -1)}{\Delta x}\right) $$ $$ \Downarrow $$ $$ sinx\cdot0=0 $$ $$ sinx \cdot \lim_{\Delta x \mapsto 0}\left(\frac{( cos\Delta x -1)}{\Delta x}\right) $$ $$ \Downarrow $$ $$ sinx\cdot0=0 $$ $$ cosx \cdot \lim_{\Delta x \mapsto 0}\left(\frac{sin\Delta x cosx}{\Delta x}\right)=cosx \cdot 1=cosx $$ $$ cosx \cdot \lim_{\Delta x \mapsto 0}\left(\frac{sin\Delta x cosx}{\Delta x}\right) $$ $$ \Downarrow $$ $$ cosx \cdot 1=cosx $$ $$ cosx \cdot \lim_{\Delta x \mapsto 0}\left(\frac{sin\Delta x cosx}{\Delta x}\right) $$ $$ \Downarrow $$ $$ cosx \cdot 1=cosx $$ Dunque $$ \frac{dsinx}{dx}=cosx $$
Da memorizzare!Tracciamo una mini carrellata delle derivate che si incontrano più spesso in un corso di fisica
$$ \frac{dK}{dx}=0 $$ $$ \frac{dx^n}{dx}=n\cdot x^{n-1} $$ $$ \frac{dlnx}{dx}=\frac{1}{x} $$ $$ \frac{de^x}{dx}=e^x $$ $$ \frac{dsinx}{dx}=cosx $$ $$ \frac{dcosx}{dx}=-sinx $$ $$ \frac{dtgx}{dx}=\frac{1}{cos^2x}=1+tg^2x $$ $$ \frac{dtgx}{dx}=\frac{1}{cos^2x}=1+tg^2x $$ $$ \frac{dtgx}{dx}=\frac{1}{cos^2x}=1+tg^2x $$
Formule per il calcolo delle derivate
Se abbiamo una funzione del tipo $$ y=Af(x) $$ La sua derivata sarà $$ \frac{dy}{dx}=A\frac{df}{dx} $$ La \(A\) è una costante rispetto a \(x\). Questa formula deriva dalle proprietà dei rapporti incrementali.
DimostrazioneDimostriamo la relazione \( \frac{dAf}{dx}=A\frac{df}{dx}\)
Calcoliamo il rapporto incrementale della funzione $$ \frac{A\cdot f(x+\Delta x)-Af(x)}{\Delta x} $$ $$ \frac{A\cdot f(x+\Delta x)-Af(x)}{\Delta x} $$ $$ \frac{A\cdot f(x+\Delta x)-Af(x)}{\Delta x} $$ Mettiamo in evidenza la \(A\) $$ A\cdot \left[\frac{f(x+\Delta x)-f(x)}{\Delta x}\right] $$ $$ A\cdot \left[\frac{f(x+\Delta x)-f(x)}{\Delta x}\right] $$ $$ A\cdot \left[\frac{f(x+\Delta x)-f(x)}{\Delta x}\right] $$ Sappiamo che il contenuto che sta dentro le parentesi quadre rappresenta il rapporto incrementale di \(f(x)\). Facendo il limite otteniamo la formula di partenza\(\square\)
Da memorizzare!Tracciamo una mini carrellata di regole di derivazione che si incontrano più spesso in un corso di fisica
$$ \frac{d}{dx}(f(x)\pm g(x))=f'(x)\pm g'(x) $$ $$ \frac{d}{dx}(f(x)\pm g(x))=f'(x)\pm g'(x) $$ $$ \frac{d}{dx}(f(x)\pm g(x)) $$ $$ \Downarrow $$ $$ f'(x)\pm g'(x) $$ $$ \frac{d}{dx}(f(x)\cdot g(x))=f'(x)g(x)+f(x)g'(x) $$ $$ \frac{d}{dx}(f(x)\cdot g(x))=f'(x)g(x)+f(x)g'(x) $$ $$ \frac{d}{dx}(f(x)\cdot g(x)) $$ $$ \Downarrow $$ $$ f'(x)g(x)+f(x)g'(x) $$ $$ \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right)=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2} $$ $$ \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right)=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2} $$ $$ \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) $$ $$ \Downarrow $$ $$ \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2} $$ $$ \frac{d}{dx}(f[g(x)])=f'[g(x)]g'(x) $$ $$ \frac{d}{dx}(f[g(x)])=f'[g(x)]g'(x) $$ $$
\frac{d}{dx}(f[g(x)]) $$ $$ \Downarrow $$ $$ f'[g(x)]g'(x) $$
Esercizi di Fisica
Film di Fisica
Formulari di Fisica
Calcolatori di Fisica
Ebook
Paradossi
Podcast
