Una funzione rappresenta una legge matematica che associa ad ogni elemento di x uno e un solo elemento di y. $$ x \mapsto y=f(x) $$ Da questa scrittura si può pensare di disegnare un sistema di assi perpendicolari tra loro. Sull'asse orizzontale mettiamo la variabile indipendente x, mentre sull'asse verticale il valore che assume la funzione.
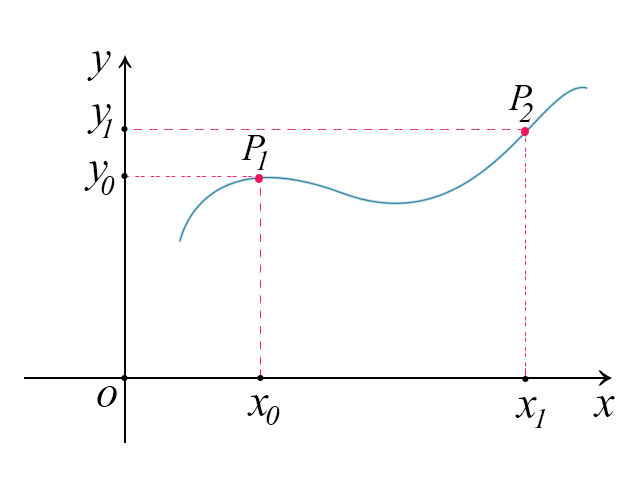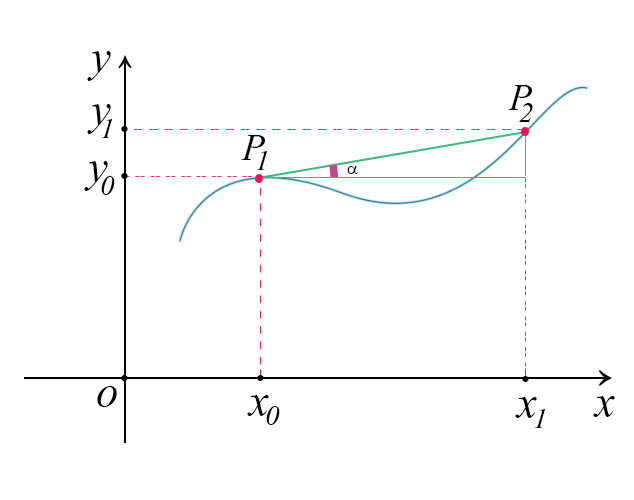
Quindi se prendiamo un punto \(x_{1}\) avremo un valore della funzione pari a \(f(x_{1})\), se prendiamo \(x_{2}\) invece avremo \(f(x_{2})\), come mostrato in figura Sul grafico appena disegnato, possiamo tracciare i punti \(P_{1}\) e \(P_{2}\) $$ P_{1}=(x_{1},f(x_{1})) $$ $$ P_{2}=(x_{2},f(x_{2})) $$ Tracciamo un segmento che unisce il punto \(P_{1}\) e il punto \(P_{2}\) e tracciamo pure il triangolo rettangolo che viene fuori dalla figura L'ipotenusa di questo triangolo, cioè c, rappresenta il segmento che unisce i due punti. Il cateto \(a\) è la lunghezza di \(\overline{x_{1}x_{2}}\) cioè la loro differenza, che chiameremo \(\Delta x\) $$ x_{2}-x_{1}=\Delta x $$ Questo valore rappresenta l'incremento da dare a \(x_{1}\) per arrivare a \(x_{2}\), cioè $$ x_{1}+\Delta x=x_{2} $$ Facciamo la stessa cosa sul cateto \(b\) del triangolo rettangolo. 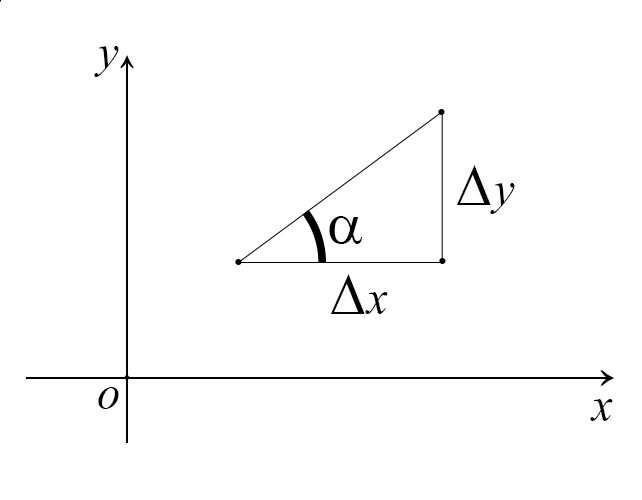Rappresenta la lunghezza del segmento \(\overline{y_{1}y_{2}}\) cioè la loro differenza, che chiameremo \(\Delta y\) $$ y_{2}-y_{1}=\Delta y $$ Questo valore rappresenta l'incremento da dare a \(y_{1}\) per arrivare a \(y_{2}\), cioè $$ y_{1}+\Delta y=y_{2} $$ Calcoliamo la tangente dell'angolo \(\alpha\) del triangolo rettangolo $$ \tan\alpha=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} $$ Questo oggetto si chiama rapporto incrementale. Noi sappiamo che, in realtà, \(y_{2}\) e \(y_{1}\) sono i valori che assume la funzione al variare della x. Possiamo dunque riscrivere la formula del rapporto incrementale come segue $$ \frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} $$ $$ \frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} $$ $$ \frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} $$ Geometricamente è la pendenza del segmento che congiunge i due punti, infatti essa è la tangente dell'angolo che forma il segmento con l'asse x Consideriamo la seguente funzione 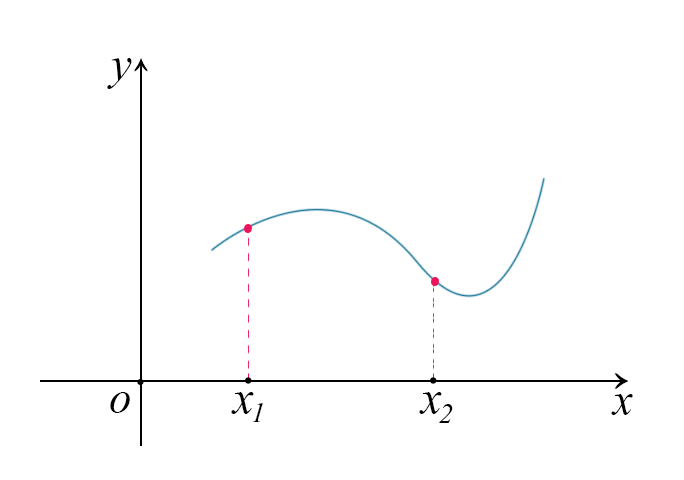Il rapporto incrementale è zero in quanto \(\Delta y\) è zero. Anche se abbiamo cambiato la variabile indipendente x, quella dipendente cioè \(y=f(x)\) non cambia.
Possiamo dunque concludere che il rapporto incrementale dipende dai punti \(x_{1}\) e \(x_{2}\) e non dalla funzione in se. Per definire bene un rapporto incrementale servono necessariamente 2 punti, \(x_{1}\) e \(x_{2}\) e bisogna anche decidere la direzione positiva dell'asse \(x\) e dell'asse \(y\).