Stima Lineare di una funzione
Consideriamo la solita funzione \(f(x)\) e tracciamo la derivata nel punto x.
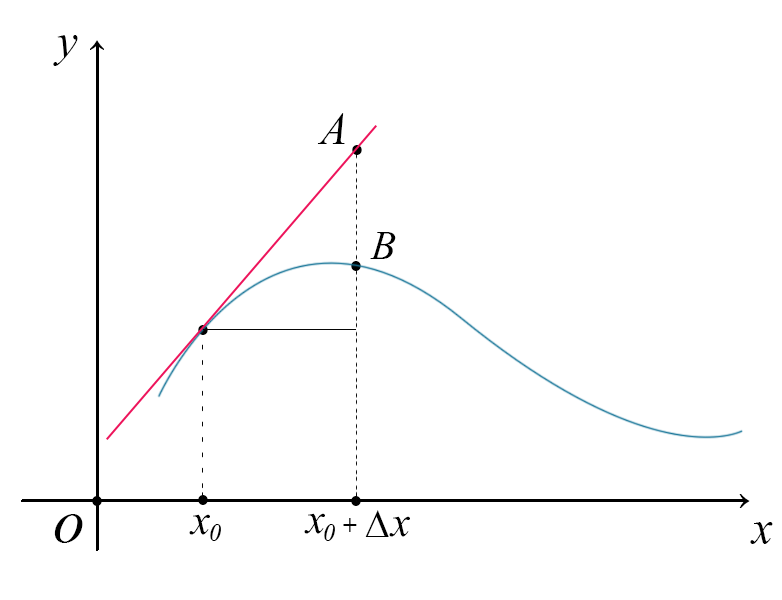
Il punto \(A\) rappresenta il prolungamento del punto \(B\) in modo da intersecare la retta tangente. \(A\) si chiama stima lineare di \(f(x+\Delta x)\), mentre il punto \(B\) è il valore vero di \(f(x+\Delta x)\).
Supponiamo di avere, fissato il punto \(x_{0}\), il valore della funzione \(f(x_{0})\) e la derivata nel punto. Conosco dunque il suo valore e la pendenza.
La domanda è: quanto vale \(f(x_{0}+\Delta x)\)?
In pratica sapendo queste due informazioni vogliamo capire cosa fa la funzione "più in là". Parliamo di stima lineare perchè stiamo usando una retta per trovare questa informazione. Ritorniamo alla figura
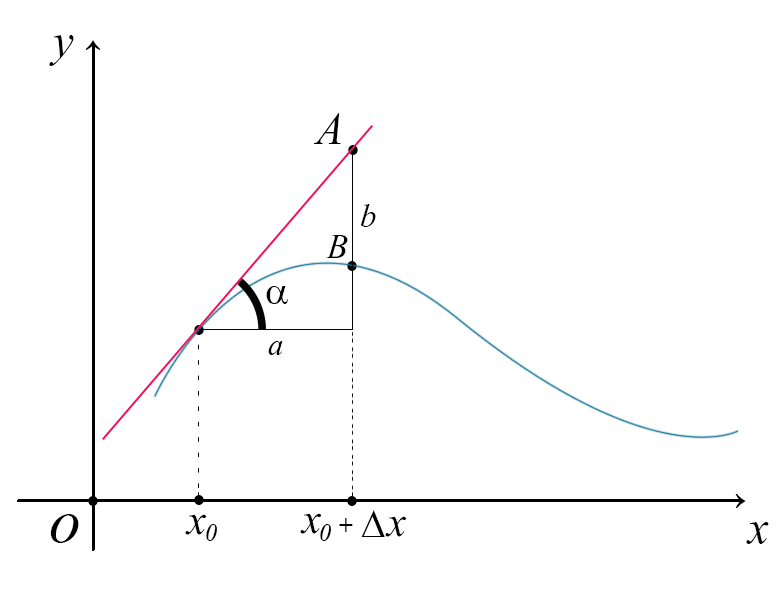
Si vede chiaramente che questa stima è pari alla somma tra il valore iniziale della funzione e il cateto \(b\) del triangolo rettangolo che si forma, in formule $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+b $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+b $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+b $$ Dalla trigonometria ricaviamo che $$ tg\alpha=\frac{b}{a}\Rightarrow b=a\cdot tg\alpha $$ Sappiamo che la tangente dell'angolo coincide con la derivata in \(x_{0}\), inoltre dalla figura si intuisce che il cateto \(a\) è \(\Delta x\) $$ tg\alpha=f'(x_{0}) $$ $$ a=\Delta x $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+f'(x_{0})\Delta x $$ $$ f_{stimalineare}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x $$ $$ f_{stimalineare}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x $$ Se abbiamo solo il valore della funzione l'unica stima sensata è $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0}) $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0}) $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0}) $$ cioè la funzione rimane costante, non ci sono i presupposti per pensarla diversamente, se non conosciamo la derivata.
Quando facciamo una stima, si incorre in errori. Se l'errore è positivo stiamo sottostimando, se è negativo stiamo sovrastimando.
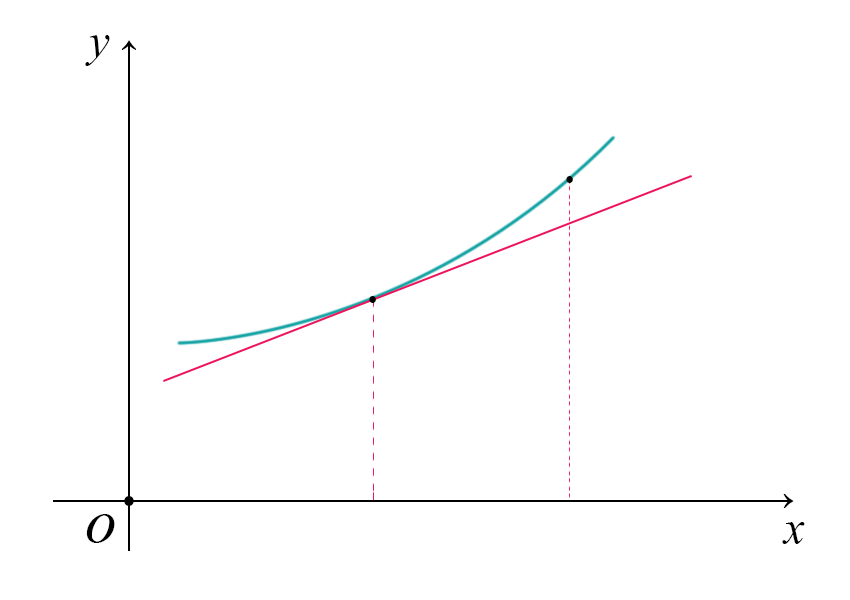
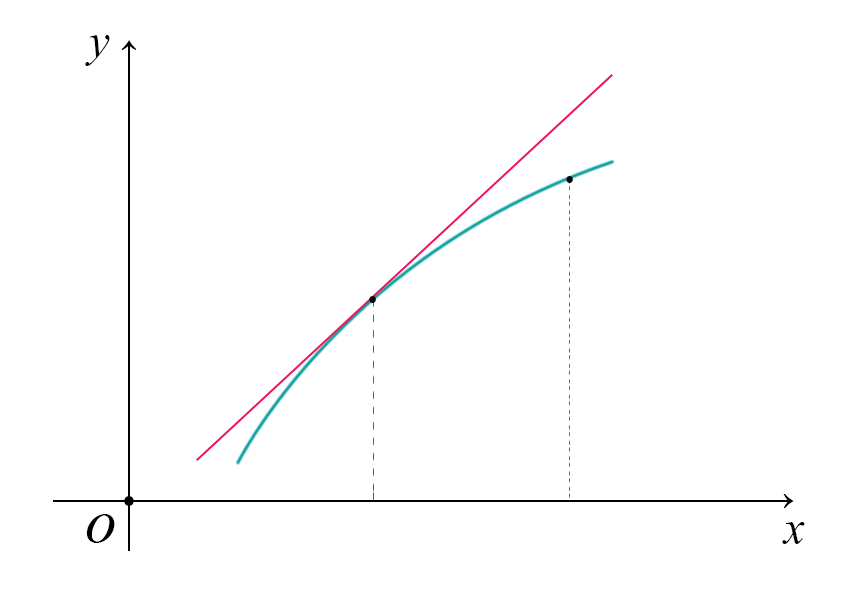
Possiamo esterndere la formula della stima lineare ad una stima più precisa, in base a quante derivate conosciamo. Usiamo dunque il famoso teorema di Taylor.
Conoscendo anche la derivata seconda della funzione, la formula di Taylor diventa $$ f_{stimaquadratica}(x_{0}+\Delta x)=f(x_{0})+f'(x_{0})\Delta x+\frac{1}{2}f''(x_{0})\Delta x^2 $$ $$ f_{stimaquadratica}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x+\frac{1}{2}f''(x_{0})\Delta x^2 $$ $$ f_{stima \\ quadratica}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x+ $$ $$ +\frac{1}{2}f''(x_{0})\Delta x^2 $$ Dove \(f''(x_{0})\) è la derivata seconda della funzione. La formula di Taylor continua conoscendo anche la derivata terza, quarta e così via.
L'errore che commettiamo facendo la stima, dipende da \(\Delta x\). Più è piccolo \(\Delta x\) più l'errore commesso diventa piccolo.
Dal teorema di Taylor ci si ferma in genere alla stima lineare, visto che il \(\Delta x\) verrà portato a 0.
 Info
Info
Funzione \(cos\alpha\)
Il coseno è una funzione pari cioè $$ cos(-\alpha)=cos\alpha $$ Infatti anche prendendo un angolo negativo, la coordinata x cioè coseno, non cambia di valore.

$$ cos\alpha=1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-\frac{\alpha^6}{6!}+... $$ $$ cos\alpha $$ $$ \Downarrow $$ $$ 1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-\frac{\alpha^6}{6!}+... $$ $$ cos\alpha $$ $$ \Downarrow $$ $$ 1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-\frac{\alpha^6}{6!}+... $$
 Info
Info
Funzione \(sin\alpha\)
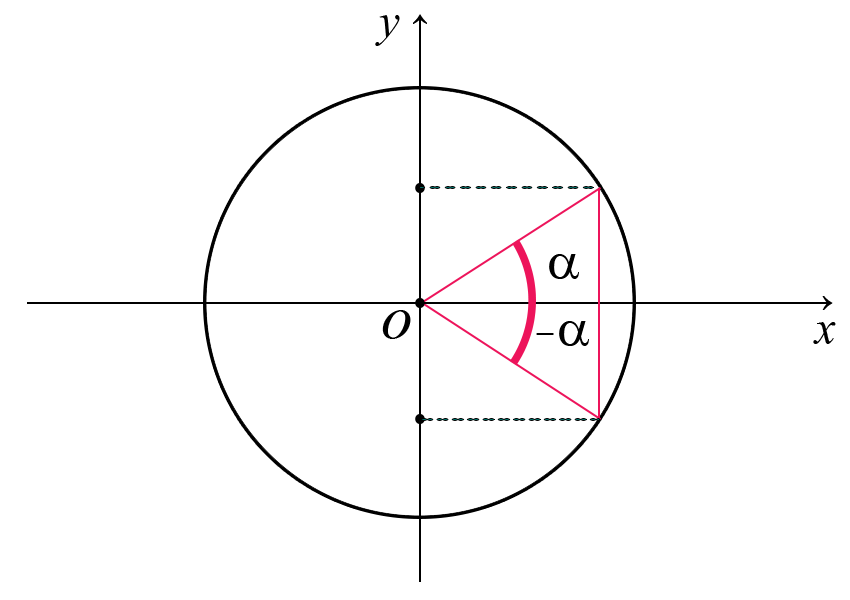
Il seno è una funzione dispari cioè $$ sin(-\alpha)=-sin\alpha $$ Essendo il seno la componente y, quando prendiamo un angolo negativo cambia di segno.
$$ sin\alpha=\alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-\frac{\alpha^7}{7!}+... $$ $$ sin\alpha $$ $$ \Downarrow $$ $$ \alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-\frac{\alpha^7}{7!}+... $$ $$ sin\alpha $$ $$ \Downarrow $$ $$ \alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-\frac{\alpha^7}{7!}+... $$
 Info
Info
Funzione \(e^x\)
$$ e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+... $$ $$ e^x $$ $$ \Downarrow $$ $$ 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+... $$ $$ e^x $$ $$ \Downarrow $$ $$ 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+... $$

Il punto \(A\) rappresenta il prolungamento del punto \(B\) in modo da intersecare la retta tangente. \(A\) si chiama stima lineare di \(f(x+\Delta x)\), mentre il punto \(B\) è il valore vero di \(f(x+\Delta x)\).
Supponiamo di avere, fissato il punto \(x_{0}\), il valore della funzione \(f(x_{0})\) e la derivata nel punto. Conosco dunque il suo valore e la pendenza.
La domanda è: quanto vale \(f(x_{0}+\Delta x)\)?
In pratica sapendo queste due informazioni vogliamo capire cosa fa la funzione "più in là". Parliamo di stima lineare perchè stiamo usando una retta per trovare questa informazione. Ritorniamo alla figura

Si vede chiaramente che questa stima è pari alla somma tra il valore iniziale della funzione e il cateto \(b\) del triangolo rettangolo che si forma, in formule $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+b $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+b $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+b $$ Dalla trigonometria ricaviamo che $$ tg\alpha=\frac{b}{a}\Rightarrow b=a\cdot tg\alpha $$ Sappiamo che la tangente dell'angolo coincide con la derivata in \(x_{0}\), inoltre dalla figura si intuisce che il cateto \(a\) è \(\Delta x\) $$ tg\alpha=f'(x_{0}) $$ $$ a=\Delta x $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0})+f'(x_{0})\Delta x $$ $$ f_{stimalineare}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x $$ $$ f_{stimalineare}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x $$ Se abbiamo solo il valore della funzione l'unica stima sensata è $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0}) $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0}) $$ $$ f_{stimalineare}(x_{0}+\Delta x)=f(x_{0}) $$ cioè la funzione rimane costante, non ci sono i presupposti per pensarla diversamente, se non conosciamo la derivata.
Quando facciamo una stima, si incorre in errori. Se l'errore è positivo stiamo sottostimando, se è negativo stiamo sovrastimando.


Possiamo esterndere la formula della stima lineare ad una stima più precisa, in base a quante derivate conosciamo. Usiamo dunque il famoso teorema di Taylor.
Conoscendo anche la derivata seconda della funzione, la formula di Taylor diventa $$ f_{stimaquadratica}(x_{0}+\Delta x)=f(x_{0})+f'(x_{0})\Delta x+\frac{1}{2}f''(x_{0})\Delta x^2 $$ $$ f_{stimaquadratica}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x+\frac{1}{2}f''(x_{0})\Delta x^2 $$ $$ f_{stima \\ quadratica}(x_{0}+\Delta x) $$ $$ \Downarrow $$ $$ f(x_{0})+f'(x_{0})\Delta x+ $$ $$ +\frac{1}{2}f''(x_{0})\Delta x^2 $$ Dove \(f''(x_{0})\) è la derivata seconda della funzione. La formula di Taylor continua conoscendo anche la derivata terza, quarta e così via.
L'errore che commettiamo facendo la stima, dipende da \(\Delta x\). Più è piccolo \(\Delta x\) più l'errore commesso diventa piccolo.
Dal teorema di Taylor ci si ferma in genere alla stima lineare, visto che il \(\Delta x\) verrà portato a 0.
Stime di Taylor di alcune funioni
Funzione \(cos\alpha\)
Il coseno è una funzione pari cioè $$ cos(-\alpha)=cos\alpha $$ Infatti anche prendendo un angolo negativo, la coordinata x cioè coseno, non cambia di valore.

$$ cos\alpha=1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-\frac{\alpha^6}{6!}+... $$ $$ cos\alpha $$ $$ \Downarrow $$ $$ 1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-\frac{\alpha^6}{6!}+... $$ $$ cos\alpha $$ $$ \Downarrow $$ $$ 1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-\frac{\alpha^6}{6!}+... $$
Funzione \(sin\alpha\)
Il seno è una funzione dispari cioè $$ sin(-\alpha)=-sin\alpha $$ Essendo il seno la componente y, quando prendiamo un angolo negativo cambia di segno.

$$ sin\alpha=\alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-\frac{\alpha^7}{7!}+... $$ $$ sin\alpha $$ $$ \Downarrow $$ $$ \alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-\frac{\alpha^7}{7!}+... $$ $$ sin\alpha $$ $$ \Downarrow $$ $$ \alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-\frac{\alpha^7}{7!}+... $$
Funzione \(e^x\)
$$ e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+... $$ $$ e^x $$ $$ \Downarrow $$ $$ 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+... $$ $$ e^x $$ $$ \Downarrow $$ $$ 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+... $$







