Una disequazione irrazionale è una disequazione dove l'incognita compare sotto il segno di radice. Per poter affrontare al meglio questo tipo di equazioni è necessario conoscere le tecniche viste per le equazioni irrazionali.
Possiamo distingure tra disequazioni irrazionali con indice pari e disequazioni irrazionali con indice pari. Le prime sono quelle più "complesse" da trattare.
Una disequazione irrazionale può apparire sotto diverse forme. Dobbiamo essere bravi noi, con una serie di passaggi algebrici, a ricondurci al seguente caso $$ \sqrt{f(x)}\gtreqless g(x) $$ Dove \(f(x)\) e \(g(x)\) sono espressioni contenenti l'incognita \(x\). Dunque dobbiamo avere un radicale da una parte e un numero o espressione con la \(x\) dall'altra parte.
Possiamo distinguere quattro casi in base al verso della disequazione:

• CASO 1 \(\rightarrow \sqrt[n]{f(x)}\geq g(x)\)
Per prima cosa sappiamo che l'argomento di una radice di indice pari deve essere sempre maggiore o uguale di zero. Inoltre non abbiamo nessuna informazione sul segno di \(g(x)\), può essere sia positivo che negativo. Se, oltre a \(f(x)\), anche \(g(x)\) è positiva allora possiamo tranquillamente elevare tutto all'indice \(n\). Ricaviamo dunque il primo sistema di disequazioni $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)\geq [g(x)]^2 \end{matrix}\right. $$ Se invece \(g(x)\) è negativa allora avremo una quantità positiva a sinistra che risulta sempre maggiore della quantità \(g(x)\). La disequazione \(\sqrt[n]{f(x)}\geq g(x)\) è automaticamente verificata. Dunque il secondo sistema è $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)< 0 \end{matrix}\right. $$ Ovviamente la soluzione della disequazione irrazionale di partenza è l'unione di questi due sistemi $$ \sqrt[n]{f(x)}\geq g(x)\iff \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)\geq [g(x)]^2 \end{matrix}\right. \cup \left\{\begin{matrix} f(x)\geq 0 \\ g(x)< 0 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}\geq g(x) $$ $$ \Updownarrow $$ $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)\geq [g(x)]^2 \end{matrix}\right. \cup \left\{\begin{matrix} f(x)\geq 0 \\ g(x)< 0 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}\geq g(x) $$ $$ \Updownarrow $$ $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)\geq [g(x)]^2 \end{matrix}\right. \cup \left\{\begin{matrix} f(x)\geq 0 \\ g(x)< 0 \end{matrix}\right. $$

• CASO 2 \(\rightarrow \sqrt[n]{f(x)}> g(x)\)
I ragionamenti visti per il caso di maggiore o uguale di zero sono gli stessi. Basterà sostituire il "\(\geq\)" con il "\(>\)" all'ultima disequazione del primo sistema. Dunque la soluzione della disequazione irrazionale sarà $$ \sqrt[n]{f(x)}> g(x)\iff \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)> [g(x)]^2 \end{matrix}\right. \cup \left\{\begin{matrix} f(x)\geq 0 \\ g(x)< 0 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}> g(x) $$ $$ \Updownarrow $$ $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)> [g(x)]^2 \end{matrix}\right. \cup \left\{\begin{matrix} f(x)\geq 0 \\ g(x)< 0 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}> g(x) $$ $$ \Updownarrow $$ $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)> [g(x)]^2 \end{matrix}\right. \cup \left\{\begin{matrix} f(x)\geq 0 \\ g(x)< 0 \end{matrix}\right. $$ In realtà in entrambi i casi, è possibile togliere la prima disequazione del primo sistema \(f(x)\geq 0\), in quanto dall'ultima disequazione del primo sistema risulta che \(f(x)\) è più grande di una quantità sicuramente positiva (visto che \(g(x)\) è elevata a potenza pari).
 Esempio
Risolvere la seguente disequazione irrazionale \( \sqrt{x^2-2}\geq x+2 \)
---
Per risolvere la disequazione dobbiamo fare l'unione dei due sistemi visti prima $$ \left\{\begin{matrix} x+2\geq 0 \\ x^2-2\geq (x+2)^2 \end{matrix}\right. \cup \left\{\begin{matrix} x^2-2\geq 0 \\ x+2< 0 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x+2\geq 0 \\ x^2-2\geq (x+2)^2 \end{matrix}\right. \cup \left\{\begin{matrix} x^2-2\geq 0 \\ x+2< 0 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x+2\geq 0 \\ x^2-2\geq (x+2)^2 \end{matrix}\right. $$ $$ \cup $$ $$ \left\{\begin{matrix} x^2-2\geq 0 \\ x+2< 0 \end{matrix}\right. $$ Svolgendo i vari calcoli abbiamo $$ \left\{\begin{matrix} x\geq -2 \\ x^2-2\geq x^2+4x+4 \end{matrix}\right. \cup \left\{\begin{matrix} x\leq -\sqrt{2} \cup x\geq\sqrt{2} \\ x< -2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x\geq -2 \\ x^2-2\geq x^2+4x+4 \end{matrix}\right. $$ $$ \cup $$ $$ \left\{\begin{matrix} x\leq -\sqrt{2} \cup x\geq\sqrt{2} \\ x< -2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x\geq -2 \\ x^2-2\geq x^2+4x+4 \end{matrix}\right. $$ $$ \cup $$ $$ \left\{\begin{matrix} x\leq -\sqrt{2} \cup x\geq\sqrt{2} \\ x< -2 \end{matrix}\right. $$ Analizziamo il primo sistema $$ \left\{\begin{matrix} x\geq -2 \\ x\leq -\frac{3}{2} \end{matrix}\right. $$


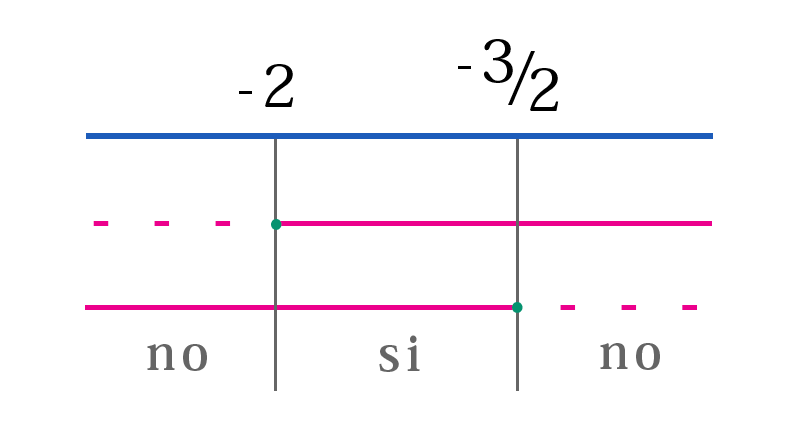
La soluzione è $$ -2\leq x\leq -\frac{3}{2} $$ Analizziamo il secondo sistema $$ \left\{\begin{matrix} x\leq -\sqrt {2}\cup x\geq \sqrt{2} \\ x< -2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x\leq -\sqrt {2}\cup x\geq \sqrt{2} \\ x< -2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} x\leq -\sqrt {2}\cup x\geq \sqrt{2} \\ x< -2 \end{matrix}\right. $$


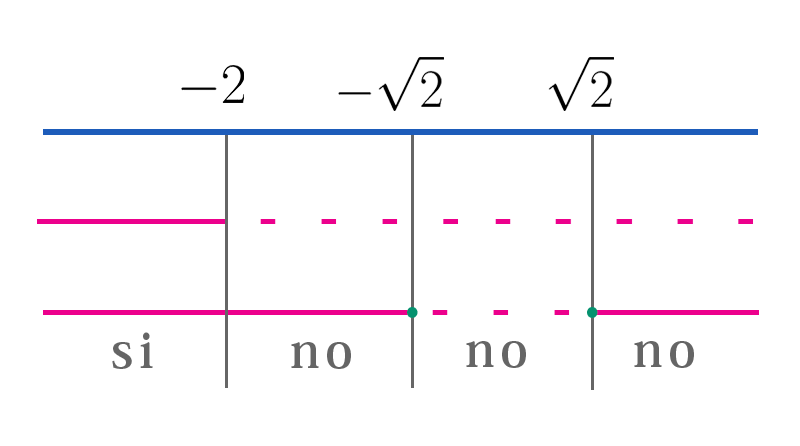
La soluzione è $$ x< -2 $$ La soluzione della disequazione irrazionale di partenza è l'unione delle soluzioni dei due sistemi


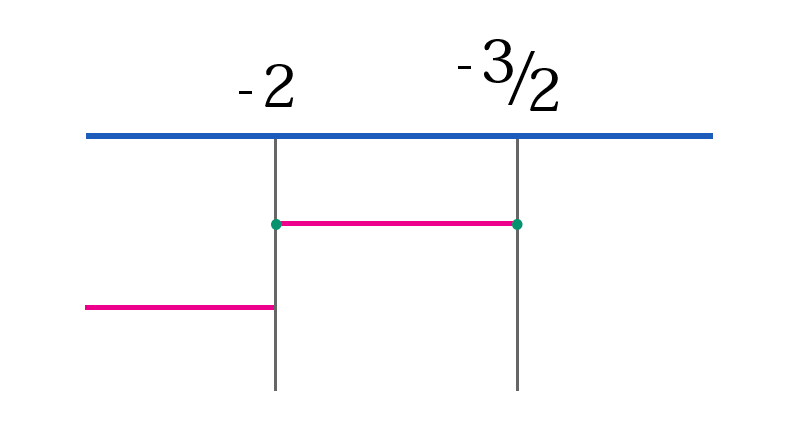
Dunque, abbiamo in definitiva $$ x\leq -\frac{3}{2} $$
• CASO 3 \(\rightarrow \sqrt[n]{f(x)}\leq g(x)\)
Per prima cosa sappiamo che l'argomento di una radice di indice pari deve essere sempre maggiore o uguale di zero. Inoltre questa volta abbiamo informazioni segno di \(g(x)\), può essere solo positivo perchè una quantità positiva o nulla (\(\sqrt{f(x)}\)) non può essere minore di una quantità negativa. La soluzione di questa disequazione è $$ \sqrt[n]{f(x)}\leq g(x)\iff \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)\leq [g(x)]^2 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}\leq g(x)\iff \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)\leq [g(x)]^2 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}\leq g(x) $$ $$ \Updownarrow $$ $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)\geq 0 \\ f(x)\leq [g(x)]^2 \end{matrix}\right. $$

• CASO 4 \(\rightarrow \sqrt[n]{f(x)}< g(x)\)
I ragionamenti sono gli stessi del caso 3. Con la differenza che \(g(x)\) non può essere nullo, deve essere strettamente positivo in quanto una quantità maggiore o uguale di zero non può essere minore di una quantità pari a zero. La soluzione di questa disequazione è $$ \sqrt[n]{f(x)}< g(x)\iff \left\{\begin{matrix} f(x)\geq 0 \\ g(x)> 0 \\ f(x)< [g(x)]^2 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}< g(x)\iff \left\{\begin{matrix} f(x)\geq 0 \\ g(x)> 0 \\ f(x)< [g(x)]^2 \end{matrix}\right. $$ $$ \sqrt[n]{f(x)}< g(x) $$ $$ \Updownarrow $$ $$ \left\{\begin{matrix} f(x)\geq 0 \\ g(x)> 0 \\ f(x)< [g(x)]^2 \end{matrix}\right. $$

---

In questo non abbiamo problemi, in quanto le radici dispari non hanno condizioni di positività, esistono sempre.